4.2. BART BMM: 2D Inputs with K Models

4.2.1. Author: John Yannotty

4.2.1.1. Date: 05/05/23

This example demonstrates the BART-BMM model on a 2-dimensional example with three different simulators. Assume the true system is defined by \(f_\dagger(x) = \sin(x_1) + \cos(x_2),\) over the domain \((x_1,x_2) \in [-\pi,\pi]\times [-\pi,\pi]\). Furthermore, consider a model set which defines \(3\) simulators under consideration in terms of Taylor series expanions of \(\sin(x_1)\) and \(\cos(x_2).\) The simulators are defined by \(h_1(x)\), \(h_2(x)\), and \(h_3(x)\) as shown below:

\[h_1(x) = \sum_{j=0}^7 \frac{s^{(j)}(x_1)}{j!}(x_1-\pi)^j + \sum_{k=0}^{10} \frac{c^{(k)}(x_2)}{k!}(x_2-\pi)^k\]

\[h_2(x) = \sum_{j=0}^{13} \frac{s^{(j)}(x_1)}{j!}(x_1+\pi)^j + \sum_{k=0}^6 \frac{c^{(k)}(x_2)}{k!}(x_2+\pi)^k\]

\[h_3(x) = \sum_{j=0}^{7} \frac{s^{(j)}(x_1)}{j!}(x_1+\pi)^j + \sum_{k=0}^8 \frac{c^{(k)}(x_2)}{k!}(x_2-\pi)^k.\]

where \(x = (x_1,x_2)\), \(s^{(j)}(x_1)\) denotes the jth derivative of \(\sin(x_1)\), and \(c^{(k)}(x_1)\) denotes the kth derivative of \(\cos(x_2)\). Each simulator is sumarized below:

• \(h_1(x)\): taylor series expansions of \(\sin(x_1)\) and \(\cos(x_2)\) about \(\pi\).

• \(h_2(x)\): taylor series expansions of \(\sin(x_1)\) and \(\cos(x_2)\) about \(-\pi\). The expansion of \(\sin(x_1)\) is a high-fidelity approximation of \(\sin(x_1)\) across the entire interval \([-\pi,\pi]\).

• \(h_3(x)\): taylor series expansions of \(\sin(x_1)\) about \(-\pi\) and \(\cos(x_2)\) about \(\pi\).

Each simulator is designed to provide a high-fidelity approximation of the true function across some subregion of the domain. For example, both terms in \(h_1(x)\) are centered about \(\pi\), hence it should provide a higher-fidelity approximation of \(f_\dagger(x)\) in the upper right corner of the domain. The objective moving forward is to combine the information across the \(3\) simulators to obtain a better global prediction and inference regarding where each model is locally accurate/inaccurate.

4.2.2. Setup

Given the setup of the problem, we can now proceed with the code required for fitting the BMM model. The subsection imports the required libraries and sets the system path for the Taweret directory. We will use the polynomial_models and trees python modules defined in Taweret for this notebook.

The polynomial_models module defines a set of toy models one can consider when testing out the Taweret software. For this example, we will be using the sin_exp, cos_exp, and sin_cos_exp which define classes for Taylor series expansions of \(\sin(x)\), \(\cos(x)\), and \(\sin(x) + \cos(x)\).

The trees module defines the BART-BMM method, which is used to combine the simulators under consideration.

# Basic imports
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import os
import random

# ! pip install Taweret    # if using Colab, uncomment to install

# Get the current directory and extract the Taweret part
# The current directory should be of the form /..../Taweret/book/notebooks/Trees
# where /.../ corresponds to your local directories.
cwd = os.getcwd()

# Get the first part of this path and append to the sys.path
tw_path = cwd.split("Taweret/")[0] + "Taweret"
sys.path.append(tw_path)

# Set the Taweret path
sys.path.append('../../../')

# Taweret imports
import Taweret.models.polynomial_models 
from Taweret.models.polynomial_models import sin_exp, cos_exp, sin_cos_exp
from Taweret.mix.trees import Trees

4.2.3. Training Data

Prior to mixing, we can generate training data over a two-dimensional grid. This is done by first generating a set of training inputs using the grid_2d_design(...) function. The function generates points with a space filling design. The 2-dimensional input space is divided into a \(n_1 \times n_2\) grid. Then, an input \(x = (x_1,x_2)\) is randomly generated in each rectangle of the grid. This results in a total of \(n = n_1n_2\) training points.

The training points are passed through the true function of \(f_\dagger(x) = \sin(x_1) + \cos(x_2)\). Then random noise is added to simulate observational data, \(Y_1,\ldots,Y_n\). The example below generates data from 80 training points, though one can easily use a smaller or larger training set.

## Functions for design points 
# n1 = number of bins in the x1 dimension
# n2 = number of bins in the x2 dimension
# n = n1*n2 is the total training size
def grid_2d_design(n1,n2, xmin = [-1,-1], xmax = [1,1]):
  # Generate n uniform rvs
  n = n1*n2
  ux = np.random.uniform(0,1,n)
  uy = np.random.uniform(0,1,n)

  # Dimensions for each rectangle
  x1_len = (xmax[0] - xmin[0])/n1
  x2_len = (xmax[1] - xmin[1])/n2
  xgrid = [[x, y] for x in range(n1) for y in range(n2)]
  xgrid = np.array(xgrid).transpose()

  # Get points
  x1 = ux*x1_len + x1_len*xgrid[0] + xmin[0]
  x2 = uy*x2_len + x2_len*xgrid[1] + xmin[1]

  # Join data
  xdata = np.array([x1,x2]).transpose()
  return xdata

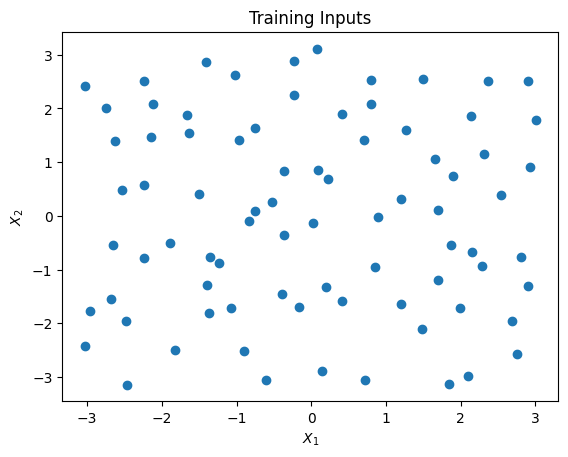
The training inputs is generated over the rectanlge \([-\pi,\pi]^2\). The design points are shown in the figure below. Then, the observational data is independently generated according to

\[Y_i \sim N(f_\dagger(x_i),\sigma^2),\]

where \(x_i = (x_{i1},x_{i2})\) is the ith training input for \(i=1,\ldots,n\). In this example, \(n = 80\).

# Generate x's 
nx1 = 10; nx2 = 8
n_train = nx1*nx2
x_train = grid_2d_design(nx1,nx2,[-np.pi,-np.pi],[np.pi,np.pi])

# Generate y's
f0_train = np.sin(x_train.transpose()[0]) + np.cos(x_train.transpose()[1])
y_train = f0_train + np.random.normal(0,0.1,n_train)

# Visualize the design points
plt.scatter(x_train.transpose()[0],x_train.transpose()[1])
plt.title("Training Inputs")
plt.xlabel("$X_1$")
plt.ylabel("$X_2$")
plt.show()

4.2.4. The Model Set

Now we can visualize the three expansions under consideration. Each surface is shown below. Note, the plots are truncated in areas where the expansion diverges. This is done only for visual purposes.

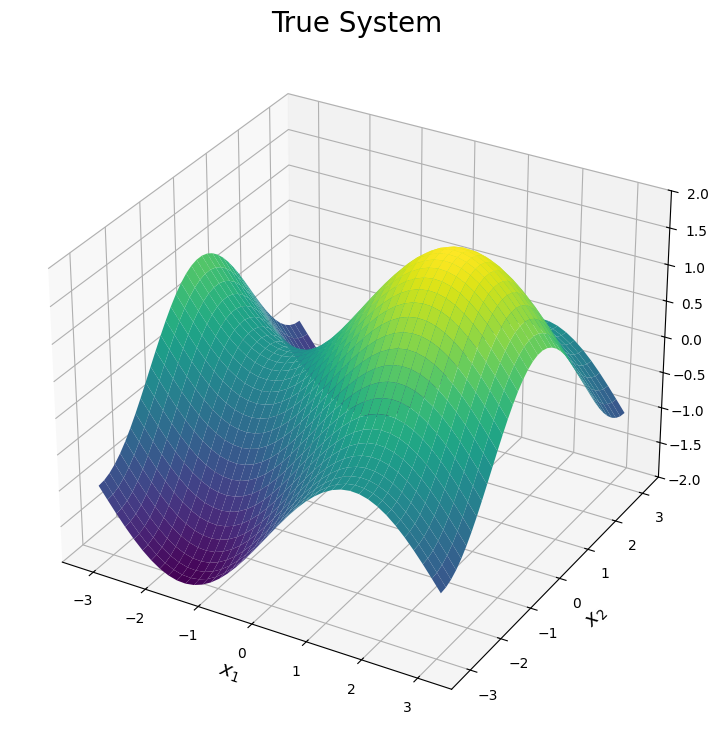
The first plot illustrates the true surface. This surface has various peaks and valleys across the input domain. We will see each simulator can be used to explain one of these features of the true surface.

# Plot the surfaces
n_test = 40
x1_test = np.outer(np.linspace(-np.pi, np.pi, n_test), np.ones(n_test))
#x1_test = np.outer(np.linspace(-3, 3, n_test), np.ones(n_test))
x2_test = x1_test.copy().transpose()
f0_test = (np.sin(x1_test) + np.cos(x2_test))
x_test = np.array([x1_test.reshape(x1_test.size,),x2_test.reshape(x1_test.size,)]).transpose()

# Define color map
cmap = plt.get_cmap('viridis')

# Creating figure
fig = plt.figure(figsize =(14, 9))
ax = plt.axes(projection ='3d')
 
# Creating plot
ax.plot_surface(x1_test, x2_test, f0_test, cmap = cmap, vmin = -2, vmax = 2)
plt.title("True System", size = 20)
plt.xlabel("$x_1$", size = 14)
plt.ylabel("$x_2$", size = 14)
ax.set_zlim([-2,2])

# show plot
plt.show()

4.2.4.1. The \(h_1(x)\) surface

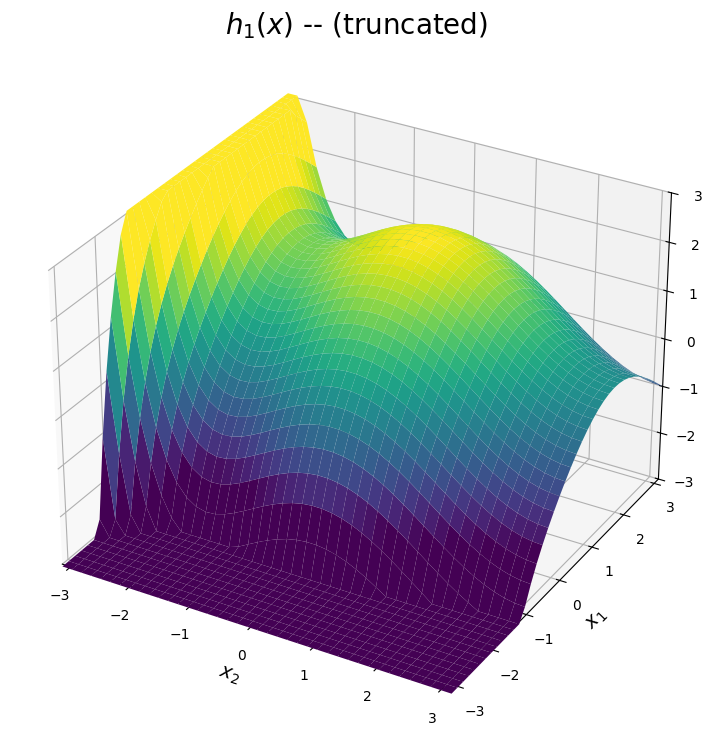
The first expansion is shown below. The predicted surface is accurate for points \((x_1,x_2)\) close to the point \((\pi,\pi)\). Based on the plot below, we can see the first expansion is designed to approximate the peak of the true system in this upper right corner of the domain. Meanwhile, the prediction diverges as \(x_1\) or \(x_2\) moves away from \(\pi\). Note for visual purposes, the plot below truncates the approximation in these diverging regions.

# Plot the first simulator
sin7 = sin_exp(7,np.pi)
cos10 = cos_exp(10,np.pi)

h1_sin = sin7.evaluate(x1_test.transpose()[0])[0]
h1_cos = cos10.evaluate(x1_test.transpose()[0])[0]

h1_sin_grid = np.outer(h1_sin, np.ones(n_test))
h1_cos_grid = np.outer(h1_cos, np.ones(n_test)).transpose()

h1_test = h1_sin_grid + h1_cos_grid

# Subset the data for the plot (only for visualization)
h1_test_filter = h1_test.copy()
for i in range(n_test):
    h1_test_filter[i][np.where(h1_test_filter[i]>3)] = 3.05
    h1_test_filter[i][np.where(h1_test_filter[i]<-3)] = -3.05
    
# Creating figure
fig = plt.figure(figsize =(14, 9))
ax = plt.axes(projection ='3d')
 
# Creating plot
ax.plot_surface(x2_test, x1_test, h1_test_filter, cmap = cmap, vmin = -2, vmax = 2)
ax.set_zlim([-3,3])
ax.set_xlim([-np.pi,np.pi])
ax.set_ylim([-np.pi,np.pi])
plt.title("$h_1(x)$ -- (truncated)", size = 20)
plt.xlabel("$x_2$", size = 14)
plt.ylabel("$x_1$", size = 14)

# show plot
plt.show()

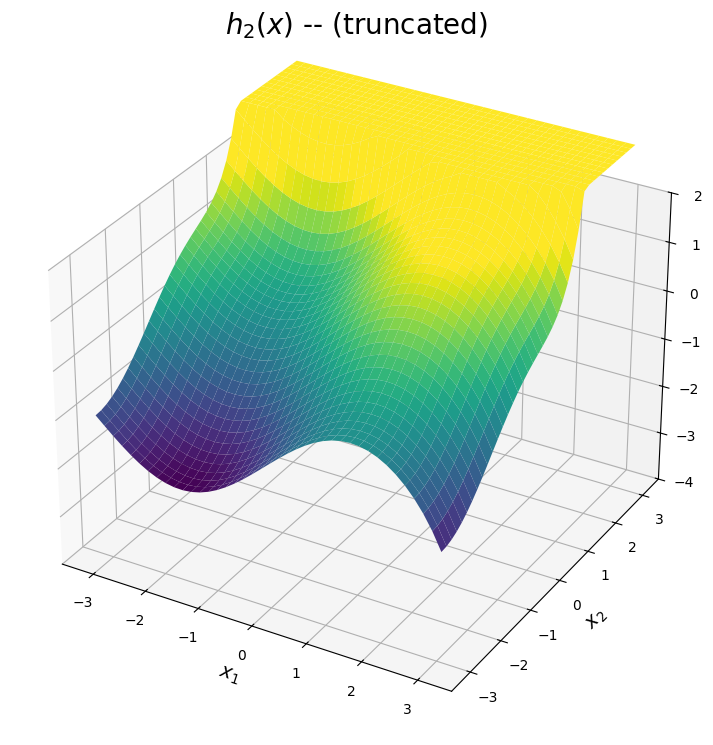
4.2.4.2. The \(h_2(x)\) surface

The second expansion is shown below. The predicted surface is accurate for points \((x_1,x_2)\) close to the point \((-\pi,-\pi)\). Additionally, the expansion of \(\sin(x_1)\) is a high-fidelity apprixmation of \(\sin(x_1)\) across the interval \([-\pi,\pi]\). Hence, from the plot below, \(h_2(x)\) can be used to approximate the valley and curvature in the true function for points in the bottom region of the domain. Once again, the surface is truncated for visual purposes in regions where the expansion diverges.

# Plot the second simulator
sin13 = sin_exp(13,-np.pi)
cos6 = cos_exp(6,-np.pi)

h2_sin = sin13.evaluate(x1_test.transpose()[0])[0]
h2_cos = cos6.evaluate(x1_test.transpose()[0])[0]

h2_sin_grid = np.outer(h2_sin, np.ones(n_test))
h2_cos_grid = np.outer(h2_cos, np.ones(n_test)).transpose()

h2_test = h2_sin_grid + h2_cos_grid

# Subset the data for the plot (only for visualization)
h2_test_filter = h2_test.copy()
for i in range(n_test):
    h2_test_filter[i][np.where(h2_test_filter[i]>3)] = 3.05
    h2_test_filter[i][np.where(h2_test_filter[i]<-3)] = -3.05


# Creating figure
fig = plt.figure(figsize =(14, 9))
ax = plt.axes(projection ='3d')
 
# Creating plot
ax.set_zlim([-4,2])
ax.plot_surface(x1_test, x2_test, h2_test_filter,cmap = cmap, vmin = -2, vmax = 2)
plt.title("$h_2(x)$ -- (truncated)", size = 20)
plt.xlabel("$x_1$", size = 14)
plt.ylabel("$x_2$", size = 14)

# show plot
plt.show()

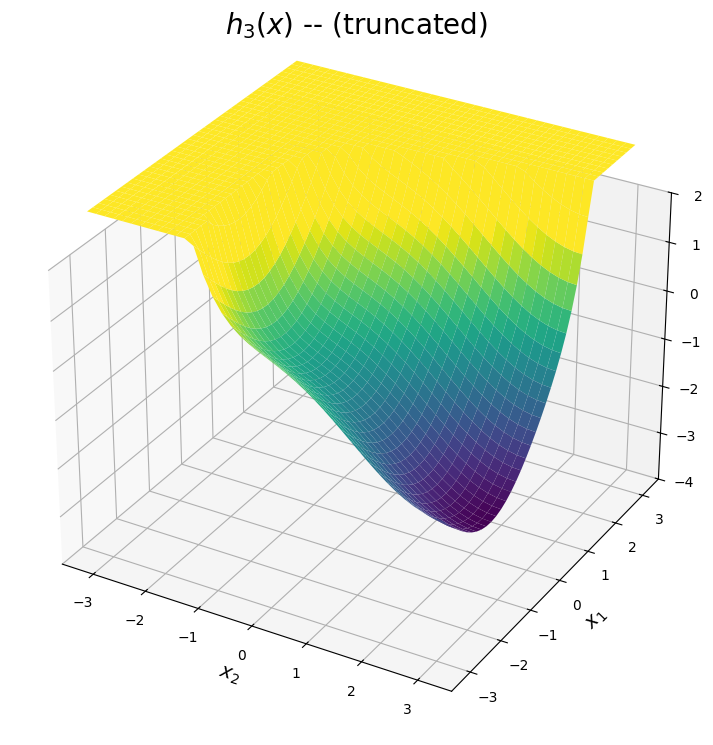
4.2.4.3. The \(h_3(x)\) surface

The third expansion is shown below. The predicted surface is accurate for points \((x_1,x_2)\) close to the point \((-\pi,\pi)\), which corresponds to the top left corner of the domain. From the plot below, this expansion can be used to approximate the valley within the upper left corner.

# Plot the second simulator
sin7_neg_pi = sin_exp(7,-np.pi)
cos8 = cos_exp(6,np.pi)

h3_sin = sin7_neg_pi.evaluate(x1_test.transpose()[0])[0]
h3_cos = cos8.evaluate(x1_test.transpose()[0])[0]

h3_sin_grid = np.outer(h3_sin, np.ones(n_test))
h3_cos_grid = np.outer(h3_cos, np.ones(n_test)).transpose()

h3_test = h3_sin_grid + h3_cos_grid

# Subset the data for the plot (only for visualization)
h3_test_filter = h3_test.copy()
for i in range(n_test):
    h3_test_filter[i][np.where(h3_test_filter[i]>3)] = 3.05
    h3_test_filter[i][np.where(h3_test_filter[i]<-3)] = -3.05


# Creating figure
fig = plt.figure(figsize =(14, 9))
ax = plt.axes(projection ='3d')
 
# Creating plot
ax.set_zlim([-4,2])
ax.plot_surface(x2_test, x1_test, h3_test_filter,cmap = cmap, vmin = -2, vmax = 2)
plt.title("$h_3(x)$ -- (truncated)", size = 20)
plt.xlabel("$x_2$", size = 14)
plt.ylabel("$x_1$", size = 14)

# show plot
plt.show()

4.2.5. The BART BMM Model

This section demonstrates how to train the BMM model for the 2D example. Note, it is assumed the software has been installed prior to running this notebook. If the software has not yet been installed, please follow the instructions under the Installation Section of the Taweret Documentation.

# Define the model set
h1 = sin_cos_exp(7,10,np.pi,np.pi)
h2 = sin_cos_exp(13,6,-np.pi,-np.pi)
h3 = sin_cos_exp(7,8,-np.pi,np.pi)
model_dict = {'model1':h1, 'model2':h2, 'model3':h3}

#h1.evaluate([[np.pi,np.pi],[-np.pi,0]])[0]
#x2_test[0:5,0:5]

# Fit the BMM Model
# Initialize the Trees class instance
mix = Trees(model_dict = model_dict)

# Set prior information
mix.set_prior(k=2.5,ntree=10,overallnu=5,overallsd=0.01,inform_prior=False)

# Train the model
fit = mix.train(X=x_train, y=y_train, ndpost = 10000, nadapt = 2000, nskip = 2000, adaptevery = 500, minnumbot = 4, numcut = 100)

Results stored in temporary path: /tmp/openbtmixing_eo9rqky2
Running model...

/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/.libs/
/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtcli

CompletedProcess(args=['mpirun', '-np', '2', '/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtcli', '/tmp/openbtmixing_eo9rqky2'], returncode=0, stdout=b'\n-----------------------------------\nOpenBT command-line interface (cli)\nLoading config file at /tmp/openbtmixing_eo9rqky2/\nnode 1 loaded 80 mixing inputs of dimension 3 from /tmp/openbtmixing_eo9rqky2/f1\nStarting MCMC...\nAdapt iteration 0\nAdapt iteration 100\nAdapt iteration 200\nAdapt iteration 300\nAdapt iteration 400\nAdapt iteration 500\nAdapt iteration 600\nAdapt iteration 700\nAdapt iteration 800\nAdapt iteration 900\nAdapt iteration 1000\nAdapt iteration 1100\nAdapt iteration 1200\nAdapt iteration 1300\nAdapt iteration 1400\nAdapt iteration 1500\nAdapt iteration 1600\nAdapt iteration 1700\nAdapt iteration 1800\nAdapt iteration 1900\nBurn iteration 0\nBurn iteration 100\nBurn iteration 200\nBurn iteration 300\nBurn iteration 400\nBurn iteration 500\nBurn iteration 600\nBurn iteration 700\nBurn iteration 800\nBurn iteration 900\nBurn iteration 1000\nBurn iteration 1100\nBurn iteration 1200\nBurn iteration 1300\nBurn iteration 1400\nBurn iteration 1500\nBurn iteration 1600\nBurn iteration 1700\nBurn iteration 1800\nBurn iteration 1900\nDraw iteration 0\nDraw iteration 100\nDraw iteration 200\nDraw iteration 300\nDraw iteration 400\nDraw iteration 500\nDraw iteration 600\nDraw iteration 700\nDraw iteration 800\nDraw iteration 900\nDraw iteration 1000\nDraw iteration 1100\nDraw iteration 1200\nDraw iteration 1300\nDraw iteration 1400\nDraw iteration 1500\nDraw iteration 1600\nDraw iteration 1700\nDraw iteration 1800\nDraw iteration 1900\nDraw iteration 2000\nDraw iteration 2100\nDraw iteration 2200\nDraw iteration 2300\nDraw iteration 2400\nDraw iteration 2500\nDraw iteration 2600\nDraw iteration 2700\nDraw iteration 2800\nDraw iteration 2900\nDraw iteration 3000\nDraw iteration 3100\nDraw iteration 3200\nDraw iteration 3300\nDraw iteration 3400\nDraw iteration 3500\nDraw iteration 3600\nDraw iteration 3700\nDraw iteration 3800\nDraw iteration 3900\nDraw iteration 4000\nDraw iteration 4100\nDraw iteration 4200\nDraw iteration 4300\nDraw iteration 4400\nDraw iteration 4500\nDraw iteration 4600\nDraw iteration 4700\nDraw iteration 4800\nDraw iteration 4900\nDraw iteration 5000\nDraw iteration 5100\nDraw iteration 5200\nDraw iteration 5300\nDraw iteration 5400\nDraw iteration 5500\nDraw iteration 5600\nDraw iteration 5700\nDraw iteration 5800\nDraw iteration 5900\nDraw iteration 6000\nDraw iteration 6100\nDraw iteration 6200\nDraw iteration 6300\nDraw iteration 6400\nDraw iteration 6500\nDraw iteration 6600\nDraw iteration 6700\nDraw iteration 6800\nDraw iteration 6900\nDraw iteration 7000\nDraw iteration 7100\nDraw iteration 7200\nDraw iteration 7300\nDraw iteration 7400\nDraw iteration 7500\nDraw iteration 7600\nDraw iteration 7700\nDraw iteration 7800\nDraw iteration 7900\nDraw iteration 8000\nDraw iteration 8100\nDraw iteration 8200\nDraw iteration 8300\nDraw iteration 8400\nDraw iteration 8500\nDraw iteration 8600\nDraw iteration 8700\nDraw iteration 8800\nDraw iteration 8900\nDraw iteration 9000\nDraw iteration 9100\nDraw iteration 9200\nDraw iteration 9300\nDraw iteration 9400\nDraw iteration 9500\nDraw iteration 9600\nDraw iteration 9700\nDraw iteration 9800\nDraw iteration 9900\nTraining time was 0.186659 minutes.\nReturning posterior, please wait...', stderr=b'')

/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/.libs/
/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtpred

CompletedProcess(args=['mpirun', '-np', '2', '/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtpred', '/tmp/openbtmixing_eo9rqky2'], returncode=0, stdout=b'\n-----------------------------------\nOpenBT prediction CLI\nLoading config file at /tmp/openbtmixing_eo9rqky2/\nnode 1 loaded 40 inputs of dimension 2 from /tmp/openbtmixing_eo9rqky2/xp1\nnode 0 loaded 40 inputs of dimension 2 from /tmp/openbtmixing_eo9rqky2/xp0\nDrawing mean response from posterior predictive\nDrawing sd response from posterior predictive\nPosterior predictive draw time was 0.00260182 minutes.\nSaving posterior predictive draws... done.\n', stderr=b'')

# Get predictions
ppost, pmean, pci, pstd = mix.predict(X = x_test, ci = 0.95)
wpost, wmean, wci, wstd = mix.predict_weights(X = x_test, ci = 0.95)

/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/.libs/
/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtpred

CompletedProcess(args=['mpirun', '-np', '2', '/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtpred', '/tmp/openbtmixing_eo9rqky2'], returncode=0, stdout=b'\n-----------------------------------\nOpenBT prediction CLI\nLoading config file at /tmp/openbtmixing_eo9rqky2/\nnode 1 loaded 800 inputs of dimension 2 from /tmp/openbtmixing_eo9rqky2/xp1\nnode 0 loaded 800 inputs of dimension 2 from /tmp/openbtmixing_eo9rqky2/xp0\nDrawing mean response from posterior predictive\nDrawing sd response from posterior predictive\nPosterior predictive draw time was 0.0382858 minutes.\nSaving posterior predictive draws... done.\n', stderr=b'')

/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/.libs/
/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtmixingwts

CompletedProcess(args=['mpirun', '-np', '2', '/home/runner/work/Taweret/Taweret/.tox/book/lib/python3.12/site-packages/openbtmixing/openbtmixingwts', '/tmp/openbtmixing_eo9rqky2'], returncode=0, stdout=b'\n-----------------------------------\nOpenBT extract mixing weights CLI\nLoading config file at /tmp/openbtmixing_eo9rqky2/\nCollecting posterior model weights\nPosterior predictive draw time was 0.0287079 minutes.\nSaving posterior weight draws... done.\n', stderr=b'')

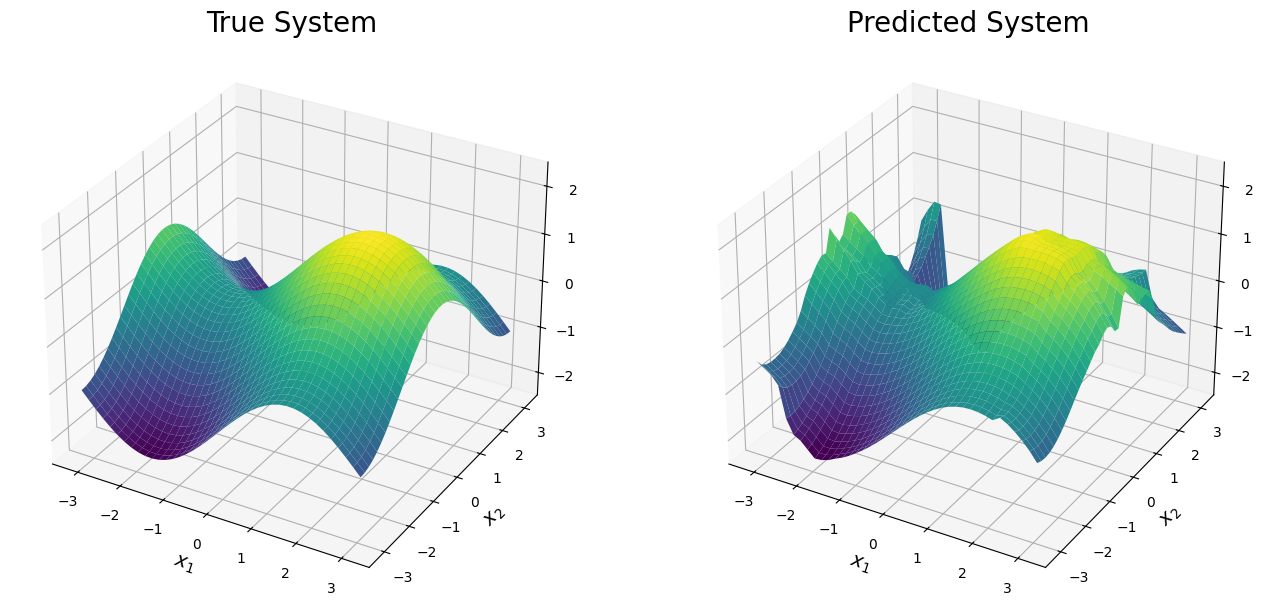
4.2.5.1. Predictions

The mean of the predicted surface from the BART-BMM model is shown below. From this plot, one can see the true surface is accurately recovered across the entire region of the domin. Since three expnansions are mixed, only 10 trees are needed to obtain such an accurate prediction.

# Creating figure
fig = plt.figure(figsize = (16,8))
ax = fig.add_subplot(1, 2, 1, projection='3d')
ax.plot_surface(x1_test, x2_test, f0_test, cmap = cmap, vmin = -2, vmax = 2)
ax.set_title("True System", size = 20)
ax.set_xlabel("$x_1$", size = 14)
ax.set_ylabel("$x_2$", size = 14)
ax.set_zlim([-2.5,2.5])

ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_surface(x1_test, x2_test, pmean.reshape(x1_test.shape), cmap = cmap, vmin = -2, vmax = 2)
ax.set_title("Predicted System", size = 20)
ax.set_xlabel("$x_1$", size = 14)
ax.set_ylabel("$x_2$", size = 14)
ax.set_zlim([-2.5,2.5])

(-2.5, 2.5)

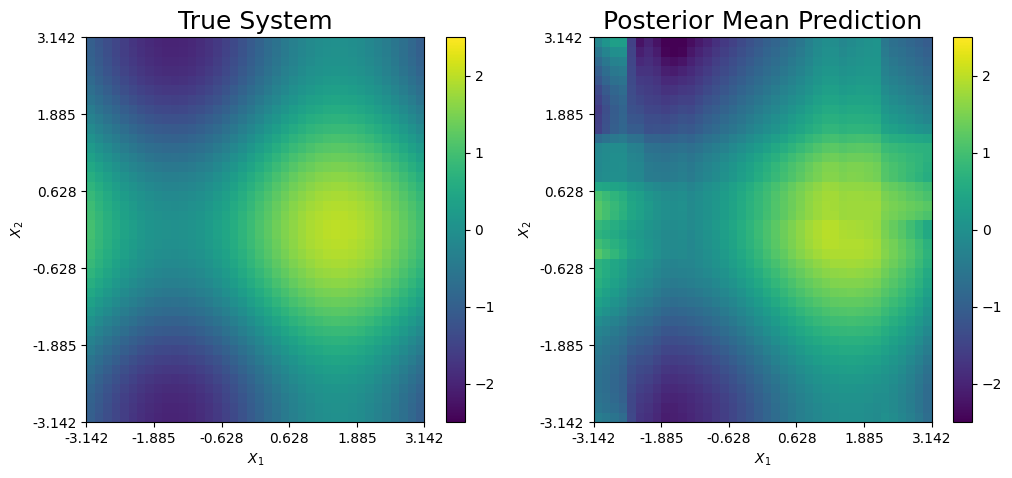
The posterior mean prediction and the true system are further compared below. Clearly, the mixed prediction combines the three expansions to accurately recover the true system. Each expansion is responsible for explaining one of the three main features of the true function.

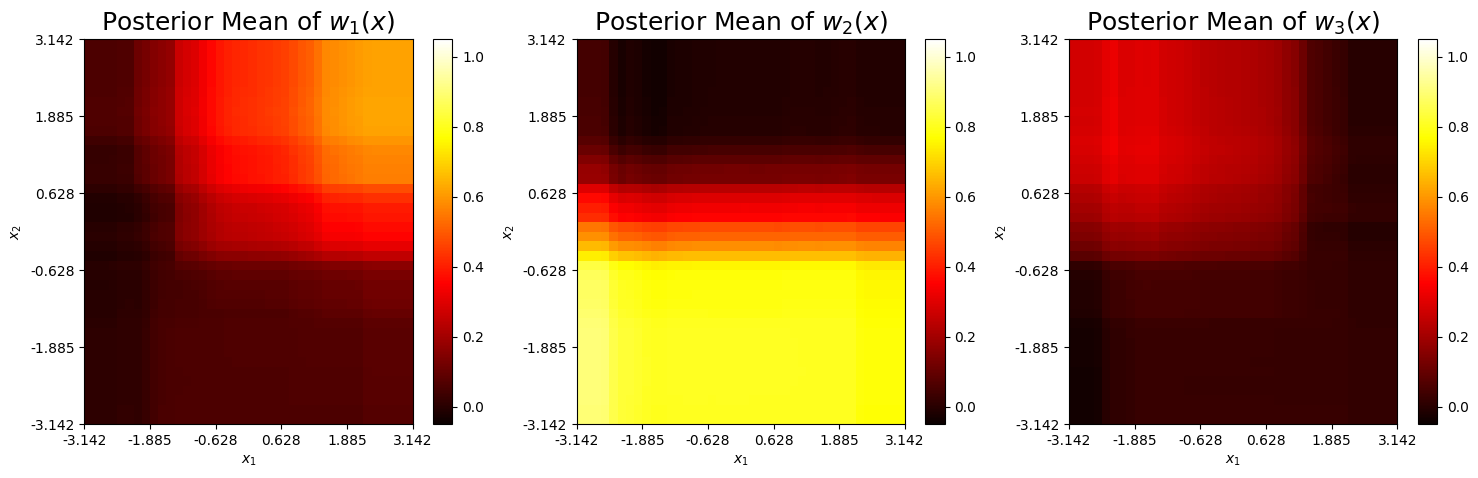
• \(h_1(x)\): Explains the peak of the system (yellow).

• \(h_2(x)\): Explains the bottom left saddle point of the system (dark blue).

• \(h_3(x)\): Explains the top right saddle point of the system (dark blue).

# Heat map comparing the surfaces
fig, ax = plt.subplots(1,2, figsize = (12,5))

pcm1 = ax[0].pcolormesh(f0_test.transpose(),cmap = cmap, vmin = -2.5, vmax = 2.5)
ax[0].set_title("True System", size = 18)
ax[0].set(xlabel = "$X_1$", ylabel = "$X_2$")
ax[0].xaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[0].xaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
ax[0].yaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[0].yaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
fig.colorbar(pcm1,ax = ax[0])


# Predicted mean
pcm2 = ax[1].pcolormesh(pmean.reshape(x1_test.shape).transpose(),cmap = cmap, vmin = -2.5, vmax = 2.5)
ax[1].set_title("Posterior Mean Prediction", size = 18)
ax[1].set(xlabel = "$X_1$", ylabel = "$X_2$")
ax[1].xaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[1].xaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
ax[1].yaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[1].yaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))

fig.colorbar(pcm2,ax = ax[1])

<matplotlib.colorbar.Colorbar at 0x7fe9e2d62a50>

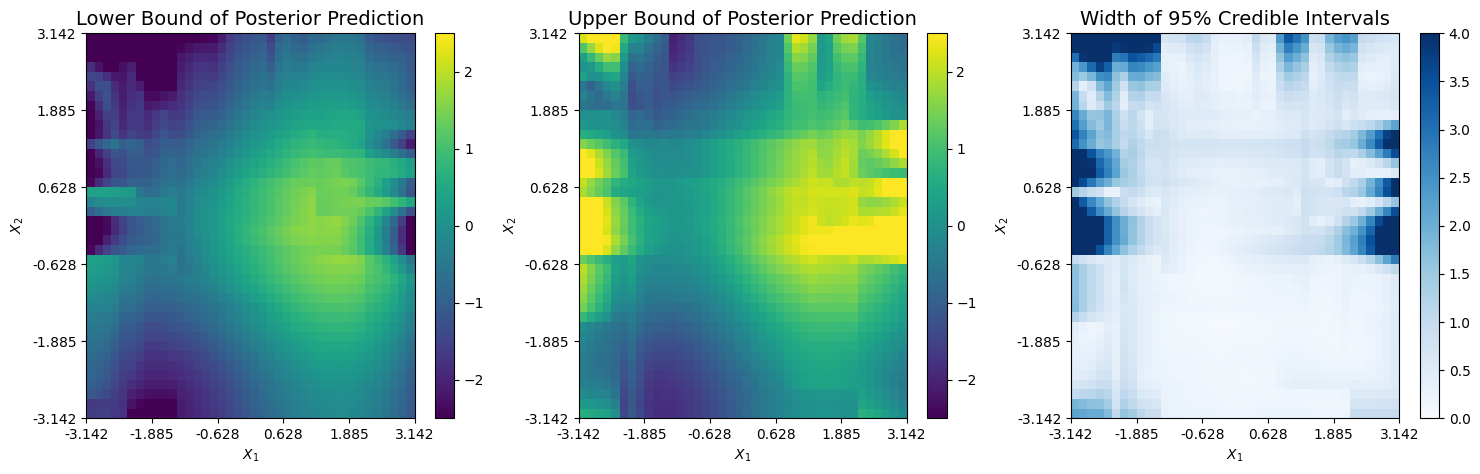
The corresponding upper and lower bounds from the 95% credible interval of the prediction are shown below. It appears non-negligible uncertainty exists only across areas where at least one expansion diverges and minimal training data is present. This typcially occurs around the boundary of the domain.

# Lower bound
cmap_blues = plt.get_cmap("Blues")
fig, ax = plt.subplots(1,3, figsize = (18,5))

pcm0 = ax[0].pcolormesh(pci[0].reshape(x1_test.shape).transpose(),cmap = cmap, vmin = -2.5, vmax = 2.5)
ax[0].set_title("Lower Bound of Posterior Prediction", size = 14)
ax[0].set(xlabel = "$X_1$", ylabel = "$X_2$")
ax[0].xaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[0].xaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
ax[0].yaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[0].yaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
fig.colorbar(pcm0,ax = ax[0])


# Upper bound
pcm1 = ax[1].pcolormesh(pci[1].reshape(x1_test.shape).transpose(),cmap = cmap, vmin = -2.5, vmax = 2.5)
ax[1].set_title("Upper Bound of Posterior Prediction", size = 14)
ax[1].set(xlabel = "$X_1$", ylabel = "$X_2$")
ax[1].xaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[1].xaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
ax[1].yaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[1].yaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
fig.colorbar(pcm1,ax = ax[1])


# CI Width
pcm2 = ax[2].pcolormesh((pci[1].reshape(x1_test.shape) - pci[0].reshape(x1_test.shape)).transpose(),cmap = cmap_blues, vmin = 0, vmax = 4)
ax[2].set_title("Width of 95% Credible Intervals", size = 14)
ax[2].set(xlabel = "$X_1$", ylabel = "$X_2$")
ax[2].xaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[2].xaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
ax[2].yaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax[2].yaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
fig.colorbar(pcm2,ax = ax[2])

<matplotlib.colorbar.Colorbar at 0x7fe9e441c710>

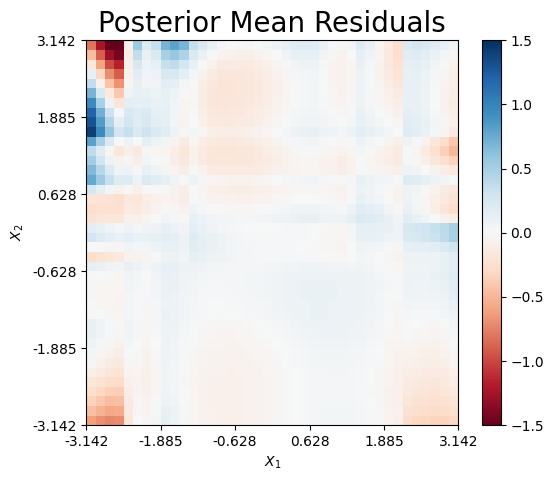
Finally, we can plot the mean residual, which is defined as \(\hat{r}(x) = f_\dagger(x) - \hat{f}_\dagger(x)\). Only minimal error exists along the boundary of the domain.

# Residual Plots
cmap_rb = plt.get_cmap("RdBu")
fig, ax = plt.subplots(1,1, figsize = (6,5))

pcm1 = ax.pcolormesh((f0_test - pmean.reshape(x1_test.shape)).transpose(),cmap = cmap_rb, vmin = -1.5, vmax = 1.5)
ax.set_title("Posterior Mean Residuals", size = 20)
ax.set(xlabel = "$X_1$", ylabel = "$X_2$")
ax.xaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax.xaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
ax.yaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
ax.yaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))

fig.colorbar(pcm1,ax = ax)

<matplotlib.colorbar.Colorbar at 0x7fe9e4794f80>

4.2.5.2. Weight Functions

The mean prediction of each weight function is shown below. Similar to the two model case, we see the weight functions take larger values in areas where the corresponding expansion is accurate. The third weight fails to take values above 0.4 in the upper left corner, which is where \(h_3(x)\) is accurate. This likely occurs because the hihg-fidelity regions of \(h_3(x)\) slighlty overlap with those from \(h_1(x)\) and \(h_2(x)\).

#sb.heatmap(wmean)
cmap_hot = plt.get_cmap('hot')

w1_mean = wmean.transpose()[0]
w1_mean = w1_mean.reshape(x1_test.shape).transpose()

w2_mean = wmean.transpose()[1]
w2_mean = w2_mean.reshape(x1_test.shape).transpose()

w3_mean = wmean.transpose()[2]
w3_mean = w3_mean.reshape(x1_test.shape).transpose()

fig, ax = plt.subplots(1,3, figsize = (18,5))
for i in range(3):
    wi_mean = wmean.transpose()[i]
    wi_mean = wi_mean.reshape(x1_test.shape).transpose()

    post_title = "Posterior Mean of $w_" + str(i+1) + "(x)$"
    pcm0 = ax[i].pcolormesh(wi_mean,cmap = cmap_hot, vmin = -0.05, vmax = 1.05)
    ax[i].set_title(post_title, size = 18)
    ax[i].set(xlabel = "$x_1$", ylabel = "$x_2$")
    ax[i].xaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
    ax[i].xaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
    ax[i].yaxis.set_major_locator(ticker.FixedLocator(np.round(np.linspace(0, n_test, 6),3)))
    ax[i].yaxis.set_major_formatter(ticker.FixedFormatter(np.round(np.linspace(-np.pi, np.pi, 6),3)))
    fig.colorbar(pcm0,ax = ax[i])

4.2.5.3. Error Standard Deviation

Finally, the posterior distribution of the error variance is shown below. The resulting posterior concentrates about the true value of 0.1. This means, the error standard deviation is accurately recovered with small uncertainty. The true value of \(\sigma = 0.10\) is accurately recovered from the BART-based model, as the posterior is nearly centered around 0.1.

# Plot the posterior of the error standard deviation
mix.plot_sigma()