Publications
Selected abstracts
(For a full list of publications see below)
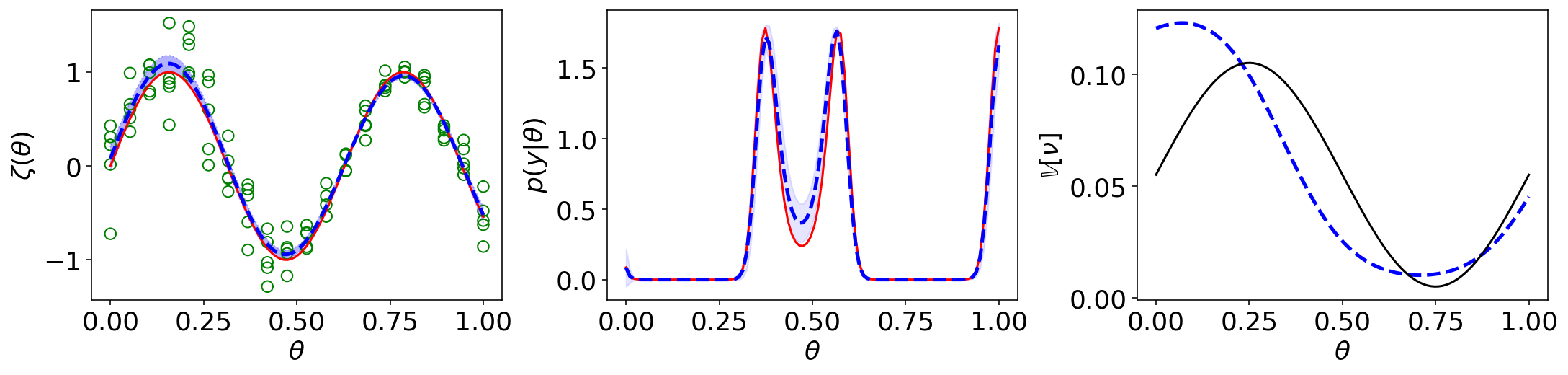
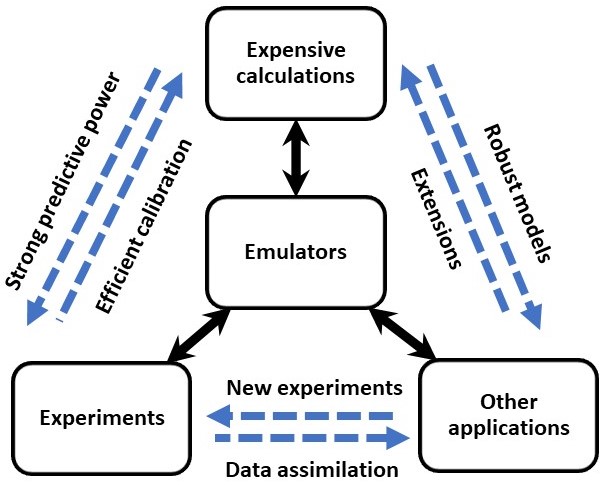
We describe the Bayesian Analysis of Nuclear Dynamics (BAND) framework, a cyberinfrastructure that we are developing which will unify the treatment of nuclear models, experimental data, and associated uncertainties. We overview the statistical principles and nuclear-physics contexts underlying the BAND toolset, with an emphasis on Bayesian methodology’s ability to leverage insight from multiple models. In order to facilitate understanding of these tools we provide a simple and accessible example of the BAND framework’s application. Four case studies are presented to highlight how elements of the framework will enable progress on complex, far-ranging problems in nuclear physics. By collecting notation and terminology, providing illustrative examples, and giving an overview of the associated techniques, this paper aims to open paths through which the nuclear physics and statistics communities can contribute to and build upon the BAND framework. [The R code used to generate the toy model figures is available as a zipfile.]
D.R. Phillips, R.J. Furnstahl, U. Heinz, T. Maiti, W. Nazarewicz, F.M. Nunes, M. Plumlee, M.T. Pratola, S. Pratt, F.G. Viens, and S.M. Wild
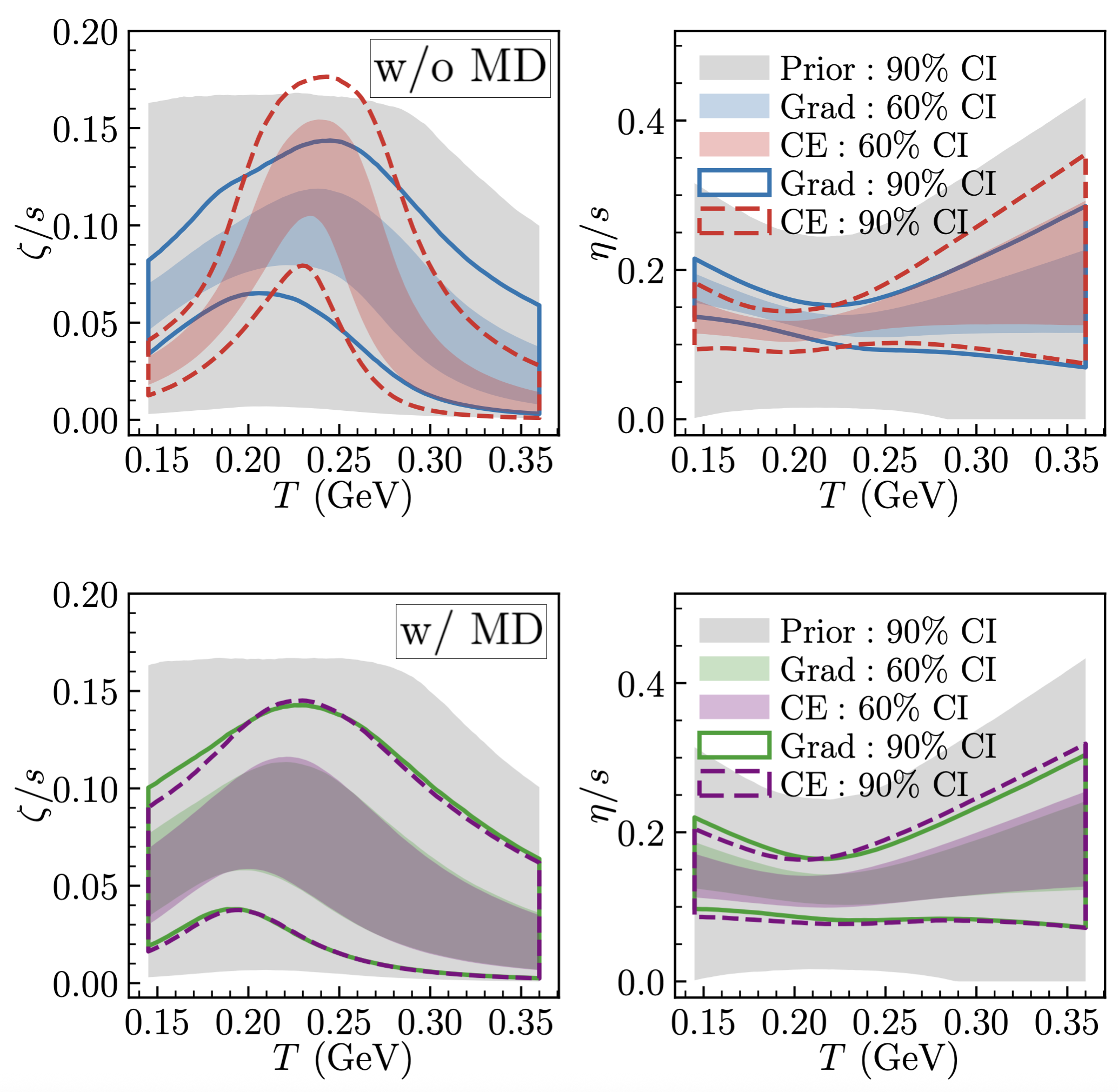
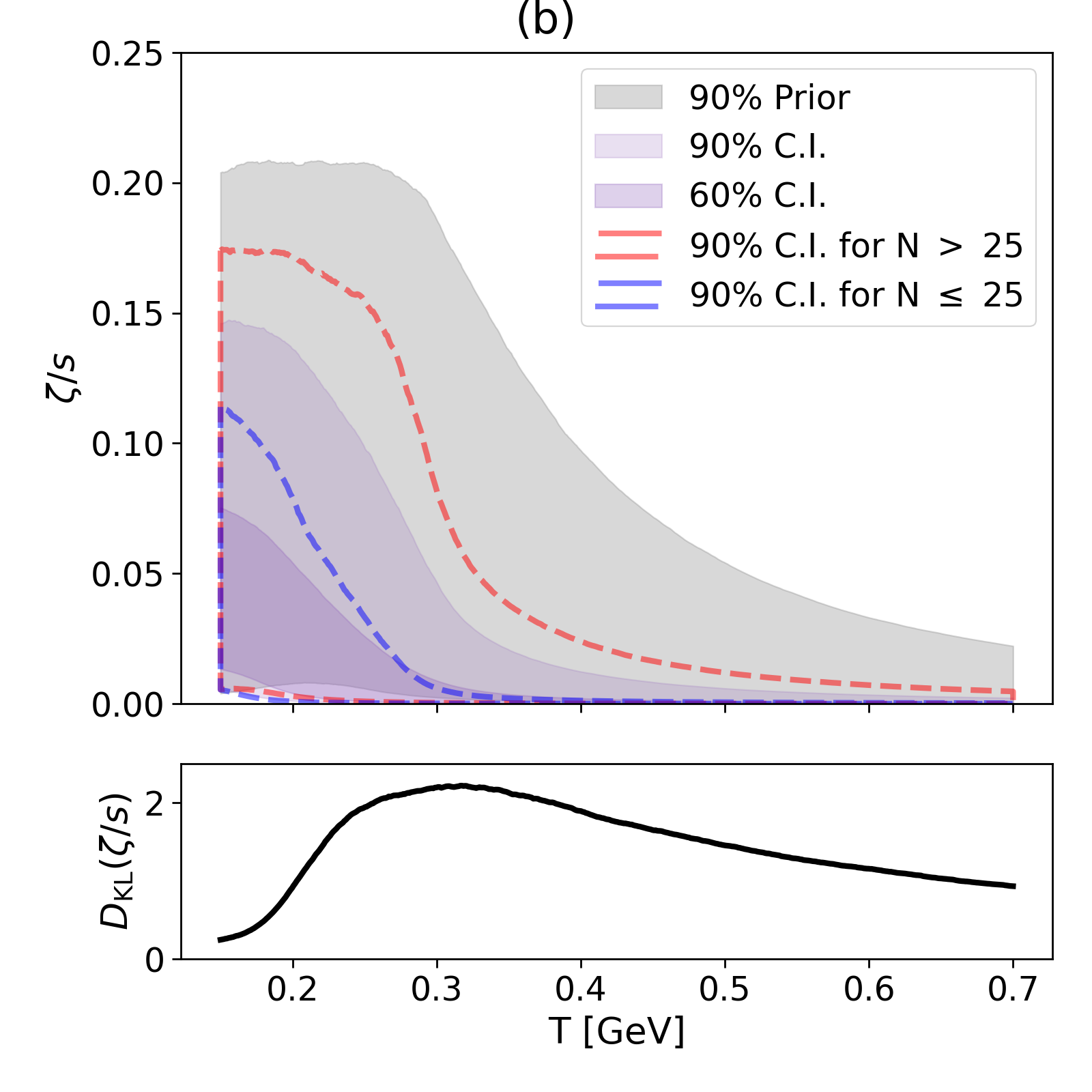
We present data-driven, state-of-the-art constraints on the temperature-dependent specific shear and bulk viscosities of the quark–gluon plasma from Pb–Pb collisions at √sₙₙ=2.76 TeV. We perform global Bayesian calibration using the JETSCAPE multistage framework with two particlization ansätze, Grad 14-moment and first-order Chapman–Enskog, and quantify theoretical uncertainties via a centrality-dependent model discrepancy term. When theoretical uncertainties are neglected, the specific bulk viscosity and some model parameters inferred using the two ansätze exhibit clear tension. Once theoretical uncertainties are quantified, the Grad and Chapman–Enskog posteriors for all model parameters become almost statistically indistinguishable and yield reliable, uncertainty-aware constraints. Furthermore, the learned discrepancy identifies where each model falls short for specific observables and centrality classes, providing insight into model limitations.
Sunil Jaiswal
Phys. Lett. B 874, 140243 (2026)
Bayesian model mixing (BMM) is a statistical technique that can combine constraints from different regions of an input space in a principled way. Here we extend our BMM framework for the equation of state (EOS) of strongly interacting matter from symmetric nuclear matter to asymmetric matter, specifically focusing on zero-temperature, charge-neutral, 𝛽-equilibrated matter. We use Gaussian processes (GPs) to infer constraints on the neutron-star matter EOS at intermediate densities from two different microscopic theories: chiral effective-field theory (𝜒EFT) at baryon densities around nuclear saturation, 𝑛𝐵∼𝑛0, and perturbative QCD at asymptotically high baryon densities, 𝑛𝐵⩾20𝑛0. The uncertainties of the 𝜒EFT and pQCD EOSs are obtained using the BUQEYE truncation error model. We demonstrate the flexibility of our framework through the use of two categories of GP kernels: conventional stationary kernels and a nonstationary changepoint kernel. We use the latter to explore potential constraints on the dense matter EOS by including exogenous data representing theory predictions and heavy-ion collision measurements at densities ⩾2𝑛0. We also use our EOSs to obtain neutron-star mass-radius relations and their uncertainties. Our framework, whose implementation will be available through a GitHub repository, provides a prior distribution for the EOS that can be used in large-scale neutron-star inference frameworks.
Alexandra C. Semposki, Christian Drischler, Richard J. Furnstahl, Daniel R. Phillips
Phys. Rev. C 113, 015808 (2026)
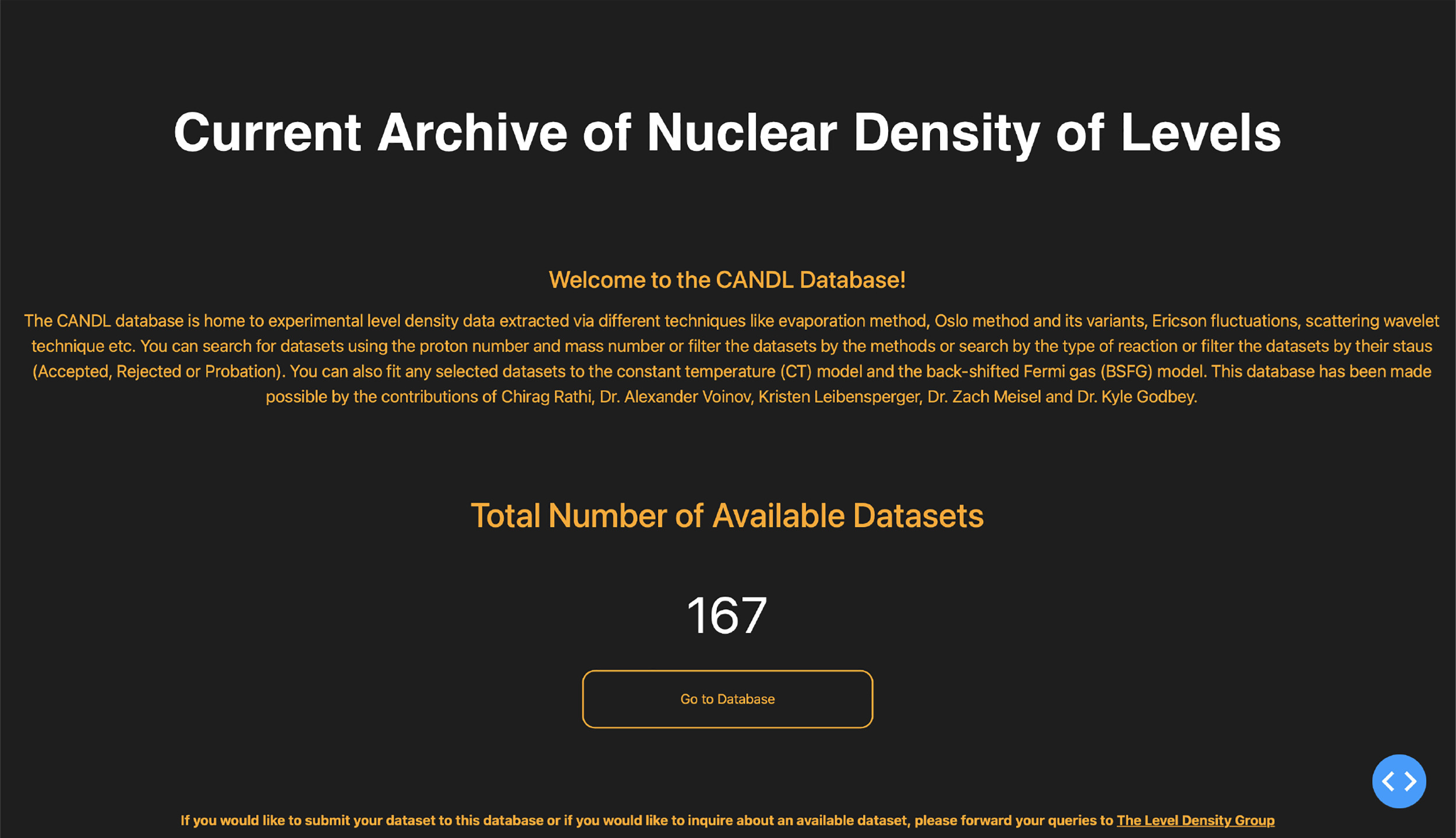
We introduce a new open-access, web-based database (https://nld.ascsn.net), Current Archive of Nuclear Density of Levels (CANDL), that hosts experimental nuclear level density (NLD) datasets from a variety of techniques and energy ranges. Built using the Dash framework in Python, the database is designed to be interactive and user-friendly, allowing researchers to search, visualize, fit, and export NLD data with minimal effort. This resource includes data extracted from evaporation spectra, Oslo method variants, and other experimental techniques that cover excitation energies beyond the neutron resonance region. The database supports on-the-fly fitting with two widely-used phenomenological models—the Constant Temperature (CT) model and the Back-Shifted Fermi Gas (BSFG) model—selected for their simplicity and computational efficiency. Future versions aim to include additional datasets and model types, as well as easy-to-use interfaces to data science techniques. This platform offers a vital tool for the nuclear physics, astrophysics, medicine, and reactor design communities.
Chirag Rathi, Alexander Voinov, Kyle Godbey, Zach Meisel, Kristen Leibensperger
Computer Physics Communications 321 (2026) 110018
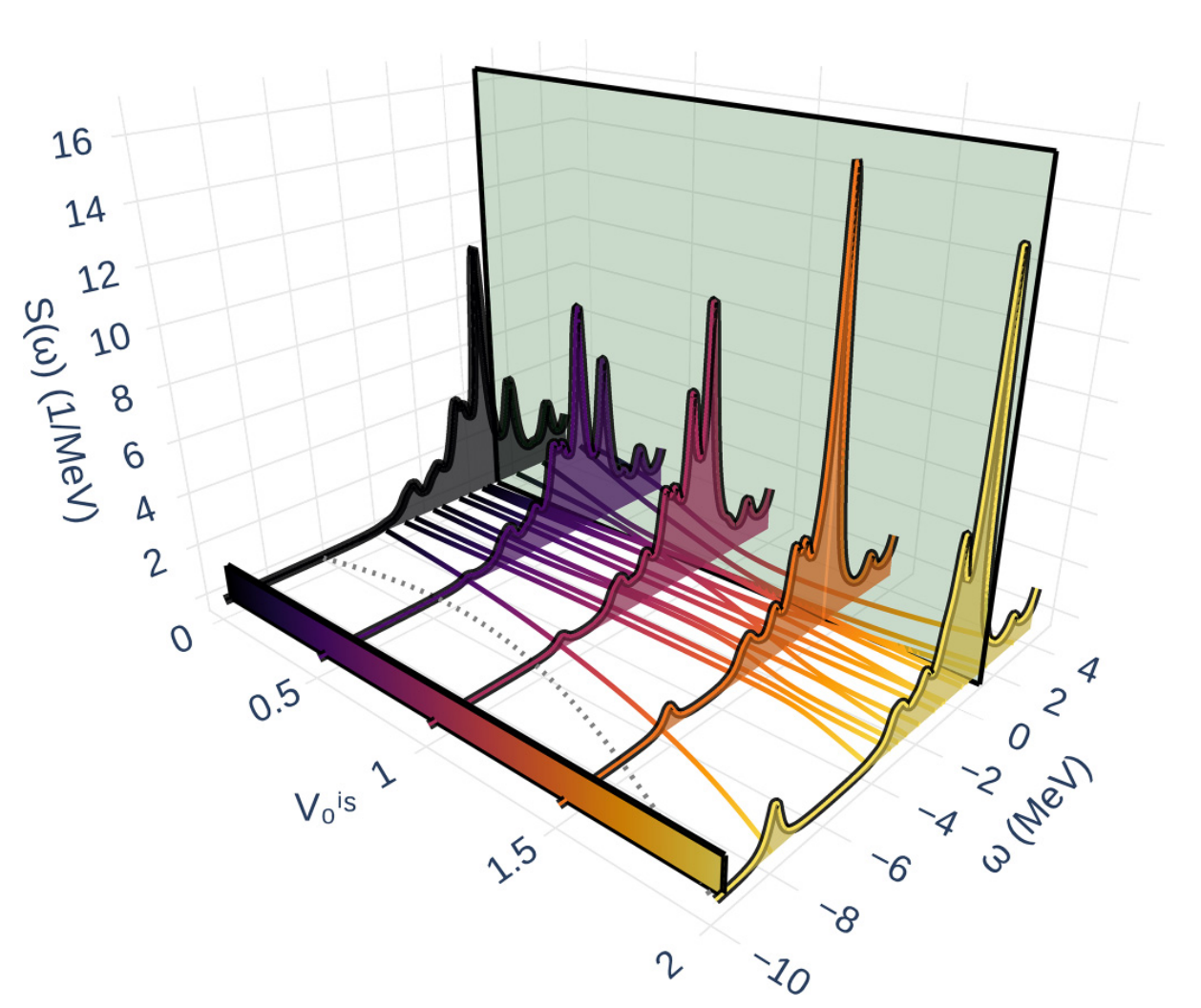
Linear response theory is a well-established method in physics and chemistry for exploring excitations of many-body systems. In particular, the quasiparticle random-phase approximation (QRPA) provides a powerful microscopic framework by building excitations on top of the mean-field vacuum; however, its high computational cost limits model calibration and uncertainty quantification studies. Here, we present two complementary QRPA surrogate models and apply them to study response functions of finite nuclei. One is a reduced-order model that exploits the underlying QRPA structure, while the other utilizes the recently developed parametric matrix model algorithm to construct a map between the system’s Hamiltonian and observables. Our benchmark applications, the calculation of the electric dipole polarizability of 180Yb and the 𝛽-decay half-life of 80Ni, show that both emulators can achieve 0.1%–1% accuracy while offering a 6–7 orders of magnitude speedup compared to state-of-the-art QRPA solvers. These results demonstrate that the developed QRPA emulators are well positioned to enable Bayesian calibration and large-scale studies of computationally expensive physics models describing the properties of many-body systems.
Lauren Jin, Ante Ravlic, Pablo Giuliani, Kyle Godbey, Witold Nazarewicz
Phys. Rev. Research 7, 043347 (2025)
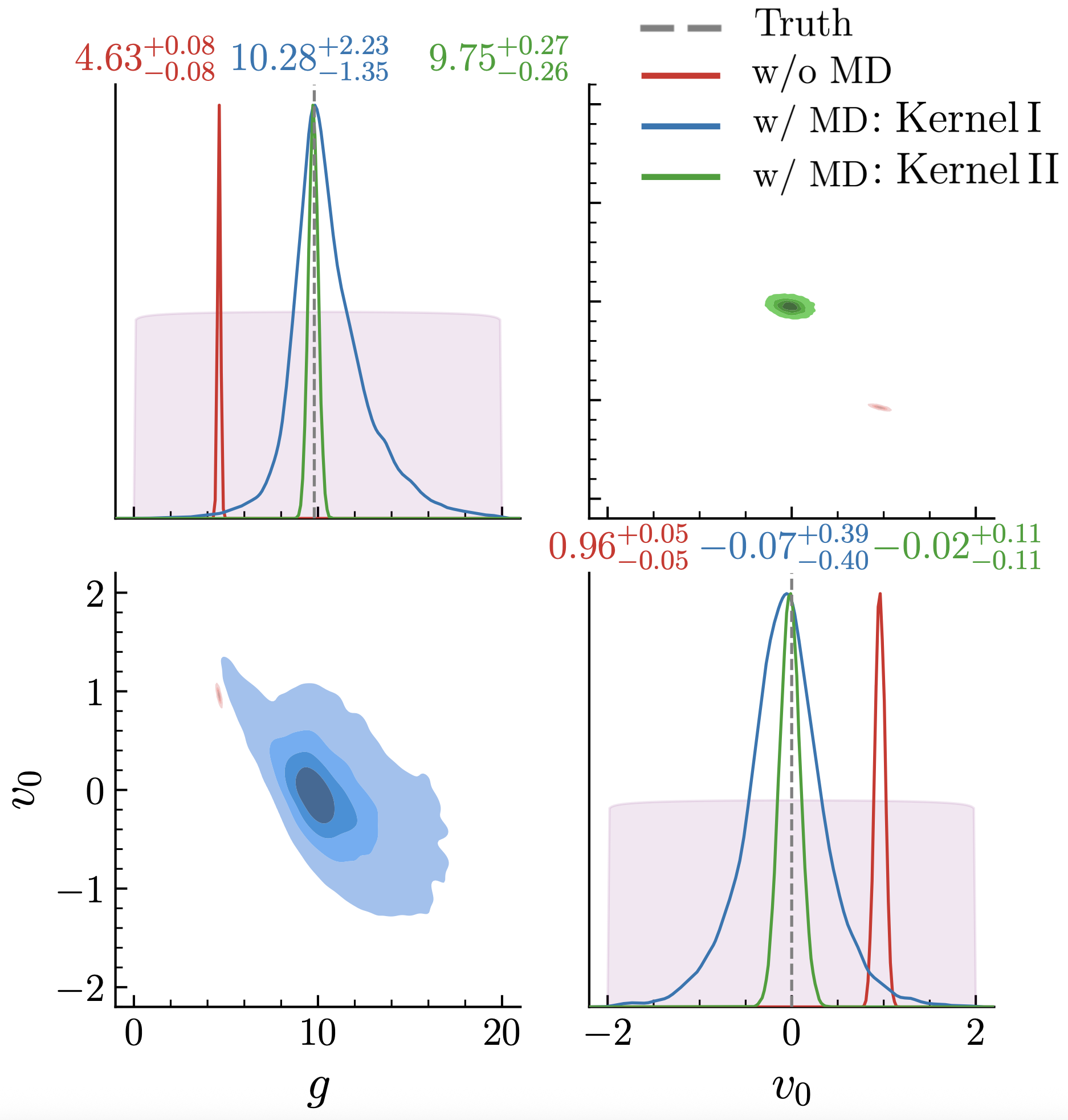
Accurate comparisons between theoretical models and experimental data are critical for scientific progress. However, inferred physical model parameters can vary significantly with the chosen physics model, highlighting the importance of properly accounting for theoretical uncertainties. In this Letter, we present a Bayesian framework that explicitly quantifies these uncertainties by statistically modeling theory errors, guided by qualitative knowledge of a theory’s varying reliability across the input domain. We demonstrate the effectiveness of this approach using two systems: a simple ball drop experiment and multi-stage heavy-ion simulations. In both cases incorporating model discrepancy leads to improved parameter estimates, with systematic improvements observed as additional experimental observables are integrated.
Sunil Jaiswal, Chun Shen, Richard J. Furnstahl, Ulrich Heinz, Matthew T. Pratola.
Phys. Lett. B 870, 139946 (2025)
The collective-flow-assisted nuclear shape-imaging method in ultrarelativistic heavy-ion collisions (UHICs) has recently been used to characterize nuclear collective states. In this paper, we assess the foundations of the shape-imaging technique employed in these studies. We argue that some current UHIC nuclear imaging techniques neglect fundamental aspects of spontaneous symmetry breaking and symmetry restoration in colliding ions and incorrectly infer one-body multipole moments from studies of nucleonic correlations. Therefore, the impact of this approach on nuclear structure research has been overstated. Conversely, efforts to incorporate existing knowledge on nuclear shapes into analysis pipelines can be beneficial for benchmarking tools and calibrating models used to extract information from ultrarelativistic heavy-ion experiments.
J. Dobaczewski, A. Gade, K. Godbey, R. V. F. Janssens, and W. Nazarewicz
Phys. Rev. Research 7, 043159 (2025)
Understanding the equation of state (EOS) of pure neutron matter is necessary for interpreting multimessenger observations of neutron stars. Reliable data analyses of these observations require well-quantified uncertainties for the EOS input. This, however, requires calculations of the EOS for a prohibitively larger number of nuclear Hamiltonians, solving the nuclear many-body problem for each one. Quantum Monte Carlo methods, such as auxiliary-field diffusion Monte Carlo (AFDMC), provide precise and accurate results for the neutron matter EOS, but they are very computationally expensive, making them unsuitable for the fast evaluations necessary for uncertainty propagation. Here, we employ parametric matrix models to develop fast emulators for AFDMC calculations of neutron matter and use them to directly propagate uncertainties of coupling constants in the Hamiltonian to the EOS. This approach provides robust uncertainty estimates for use in astrophysical data analyses, so enabling novel applications such as using astrophysical observations to put constraints on coupling constants for nuclear interactions.
Cassandra L. Armstrong, Pablo Giuliani, Kyle Godbey, Rahul Somasundaram, and Ingo Tews.
Phys. Rev. Lett. 135, 142501 (2025)
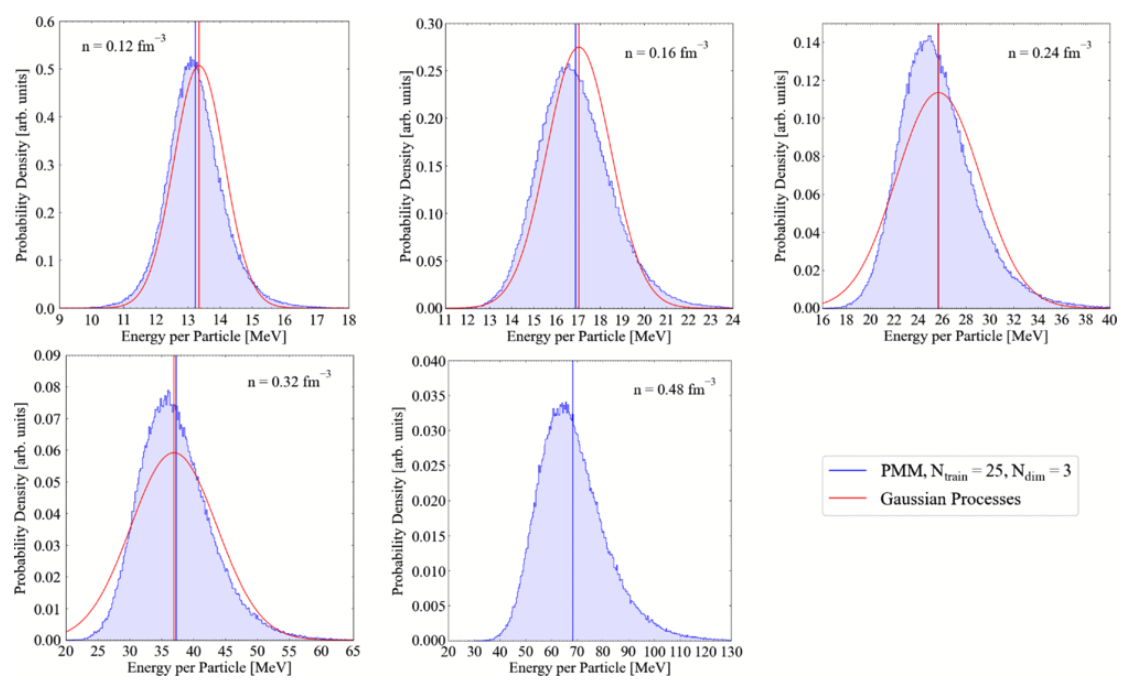
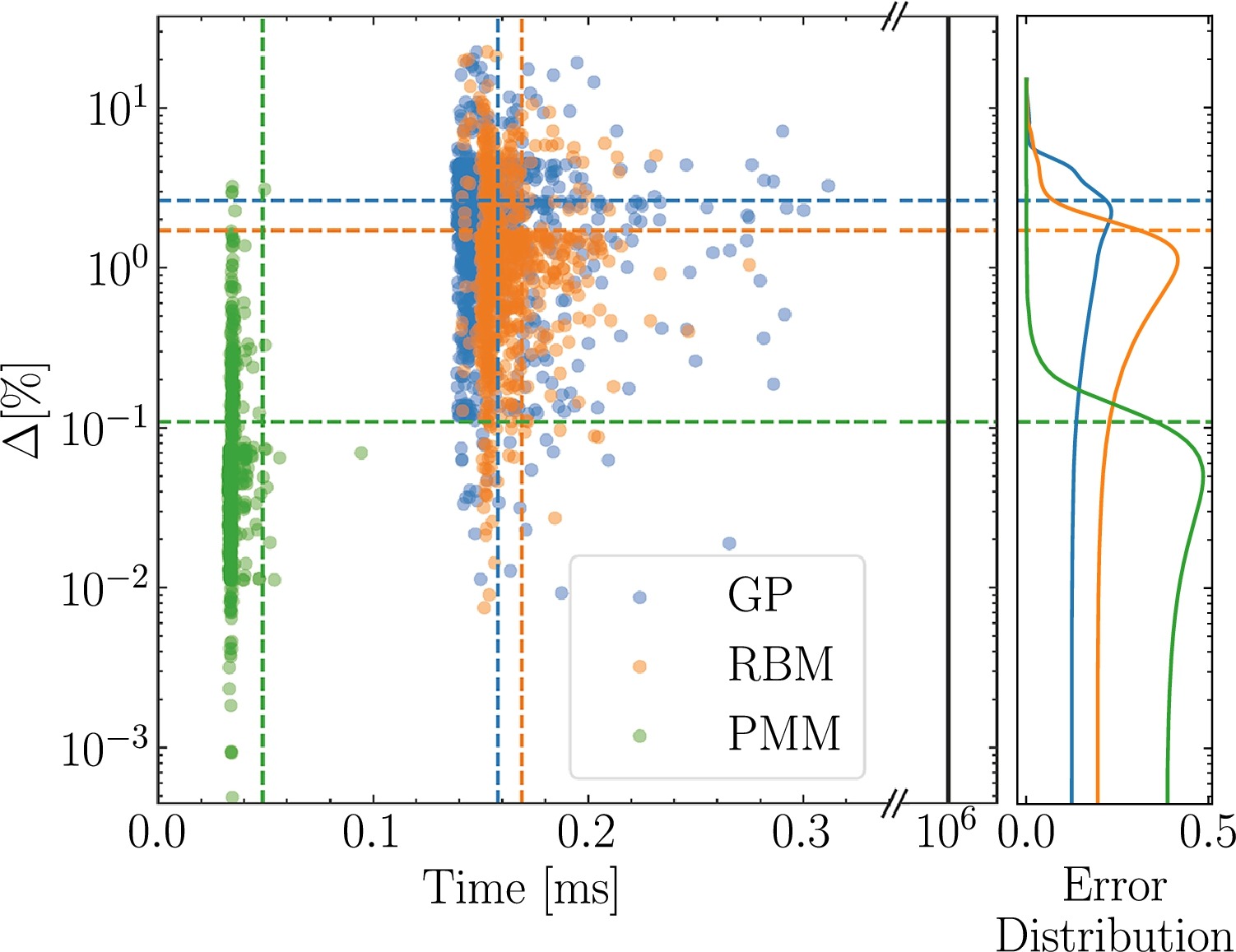
The validation, verification, and uncertainty quantification of computationally expensive theoretical models of quantum many-body systems require the construction of fast and accurate emulators. In this work, we develop emulators for auxiliary field diffusion Monte Carlo (AFDMC), a powerful many-body method for nuclear systems. We introduce a reduced-basis method (RBM) emulator for AFDMC and study it in the simple case of the deuteron. Furthermore, we compare our RBM emulator with the recently proposed parametric matrix model (PMM). We contrast these two approaches with a traditional Gaussian Process emulator. All three emulators constructed here are based on a very limited set of 5 training points, as expected for realistic AFDMC calculations, but validated against about 1000 exact solutions. We find that the PMM outperforms our implementation of the other two emulators when applied to AFDMC.
Rahul Somasundaram, Cassandra L. Armstrong, Pablo Giuliani, Kyle Godbey, Stefano Gandolfi, and Ingo Tews.
Phys. Lett. B 866, 139558 (2025)
This white paper is the result of a collaboration by many of those that attended a workshop at the facility for rare isotope beams (FRIB), organized by the FRIB Theory Alliance (FRIB-TA), on ‘Theoretical Justifications and Motivations for Early High-Profile FRIB Experiments’. It covers a wide range of topics related to the science that will be explored at FRIB. After a brief introduction, the sections address: section 2: Overview of theoretical methods, section 3: Experimental capabilities, section 4: Structure, section 5: Near-threshold Physics, section 6: Reaction mechanisms, section 7: Nuclear equations of state, section 8: Nuclear astrophysics, section 9: Fundamental symmetries, and section 10: Experimental design and uncertainty quantification.
B. Alex Brown, Alexandra Gade, S. Ragnar Stroberg, Jutta E. Escher, Kevin Fossez, Pablo Giuliani, Calem R. Hoffman, Witold Nazarewicz, et al.
J. Phys. G Nucl. Part. Phys. 52 050501 (2025)
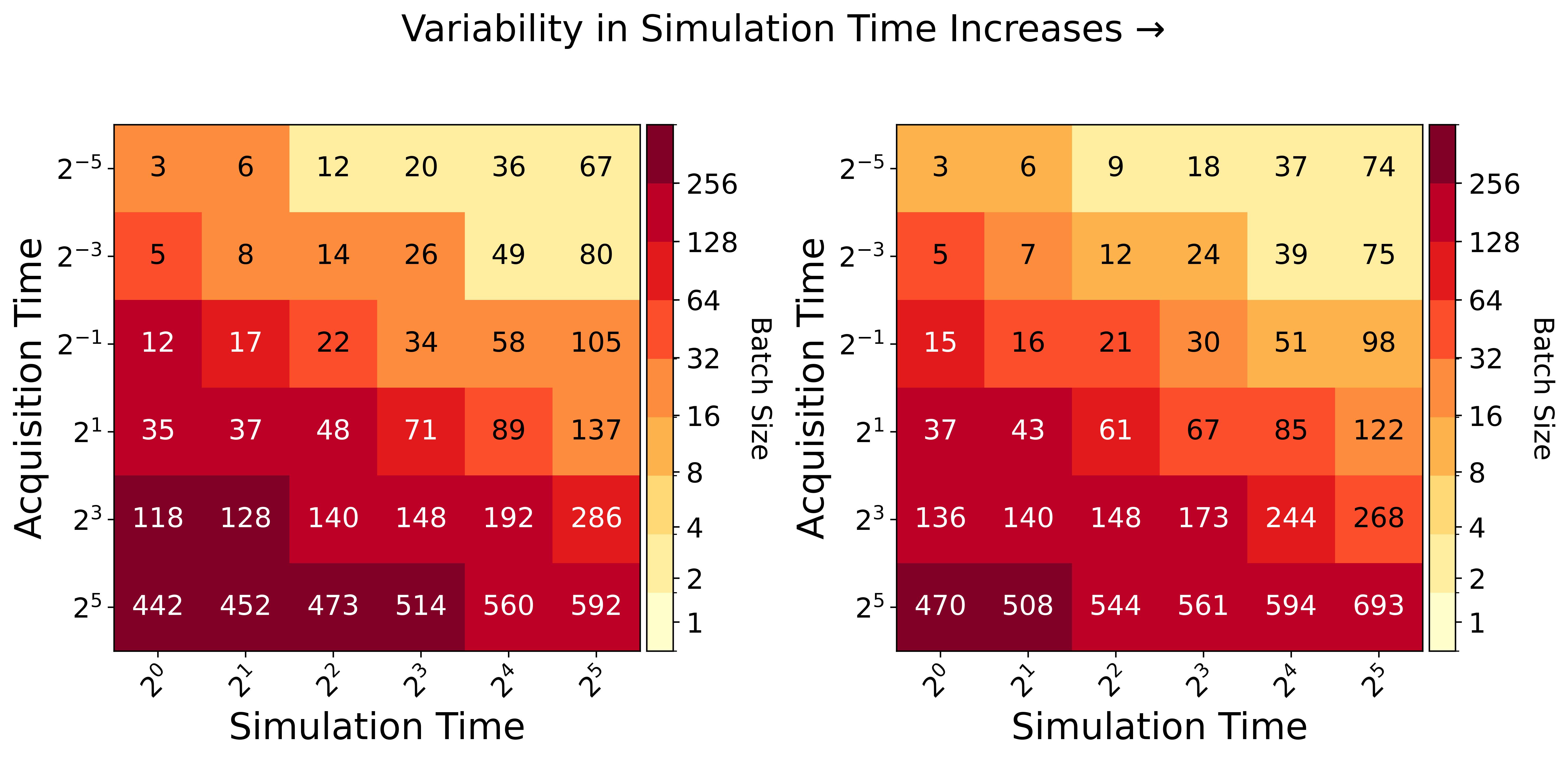
Calibration of expensive simulation models involves an emulator based on simulation outputs generated across various parameter settings to replace the actual model. Noisy outputs of stochastic simulation models require many simulation evaluations to understand the complex input-output relationship effectively. Sequential design with an intelligent data collection strategy can improve the efficiency of the calibration process. The growth of parallel computing environments can further enhance calibration efficiency by enabling simultaneous evaluation of the simulation model at a batch of parameters within a sequential design. This article proposes novel criteria that determine if a new batch of simulation evaluations should be assigned to existing parameter locations or unexplored ones to minimize the uncertainty of posterior prediction. Analysis of several simulated models and real-data experiments from epidemiology demonstrates that the proposed approach results in improved posterior predictions.
Özge Sürer.
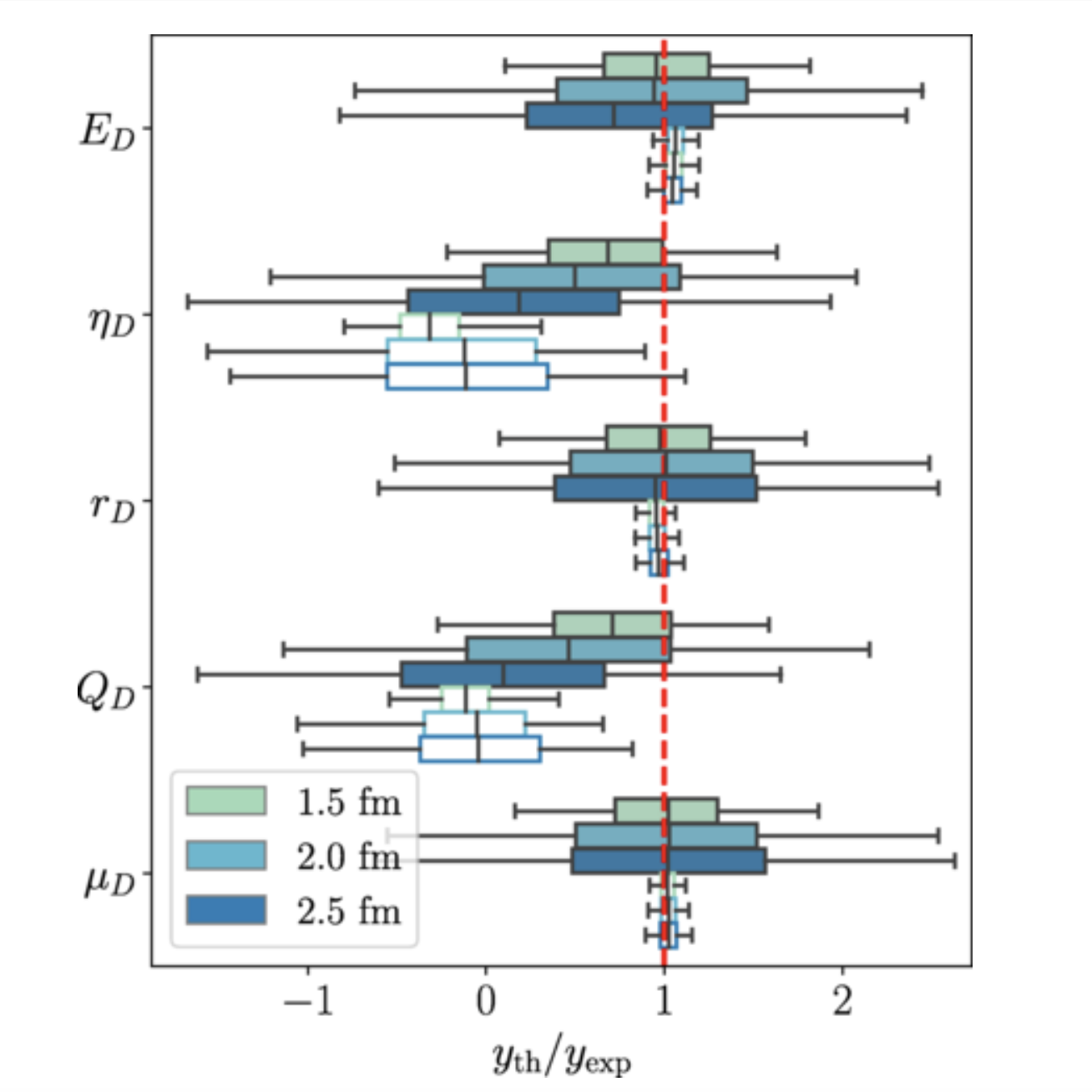
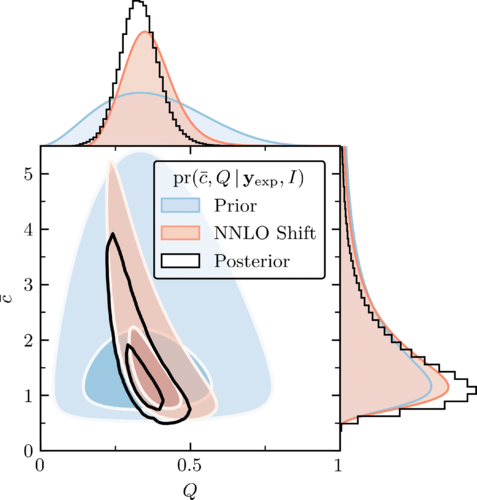
Constraining the equation of state (EOS) of strongly interacting, dense matter is the focus of intense experimental, observational, and theoretical effort. Chiral effective field theory (ChEFT) can describe the EOS between the typical densities of nuclei and those in the outer cores of neutron stars while perturbative QCD (pQCD) can be applied to properties of deconfined quark matter, both with quantified theoretical uncertainties. However, describing the full range of densities in between with a single EOS that has well-quantified uncertainties is a challenging problem. Bayesian multi-model inference from ChEFT and pQCD can help bridge the gap between the two theories. In this work, we introduce a correlated Bayesian model mixing framework that uses a Gaussian Process (GP) to assimilate different information into a single QCD EOS for symmetric nuclear matter. The present implementation uses a stationary GP to infer this mixed EOS solely from the EOSs of ChEFT and pQCD while accounting for the truncation errors of each theory. The GP is trained on the pressure as a function of number density in the low- and high-density regions where ChEFT and pQCD are, respectively, valid. We impose priors on the GP kernel hyperparameters to suppress unphysical correlations between these regimes. This, together with the assumption of stationarity, results in smooth ChEFT-to-pQCD curves for both the pressure and the speed of sound. We show that using uncorrelated mixing requires uncontrolled extrapolation of at least one of ChEFT or pQCD into regions where the perturbative series breaks down and leads to an acausal EOS. We also discuss extensions of this framework to non-stationary and less differentiable GP kernels, its future application to neutron-star matter, and the incorporation of additional constraints from nuclear theory, experiment, and multi-messenger astronomy.
A. C. Semposki, C. Drischler, R. J. Furnstahl, J. A. Melendez, D. R. Phillips
Phys. Rev. C 111, 035804 (2025)
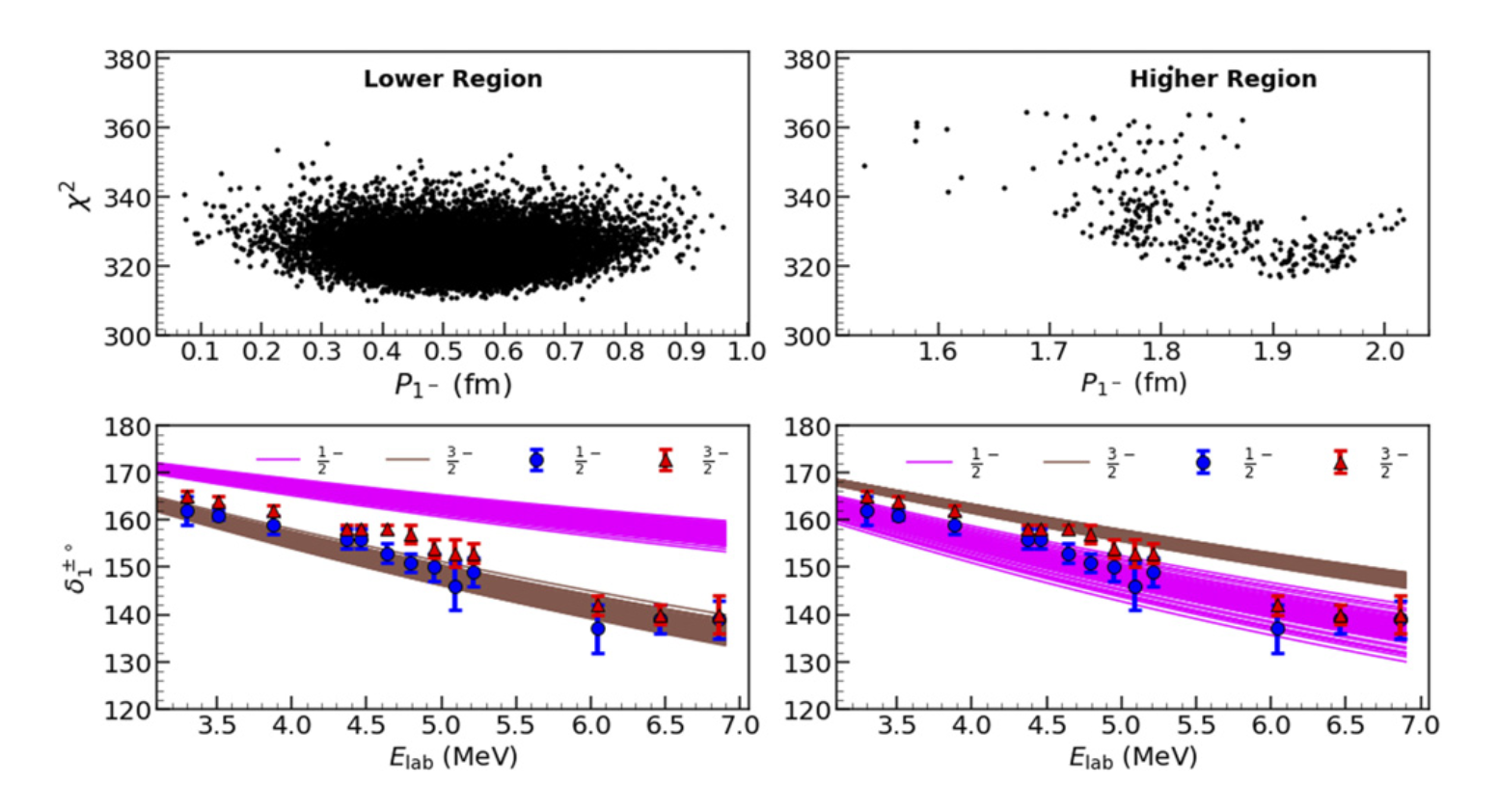
We perform Bayesian model calibration of two-nucleon (𝑁𝑁) low-energy constants (LECs) appearing in an 𝑁𝑁 interaction based on pionless effective field theory. The calibration is carried out for potentials constructed using naive dimensional analysis in 𝑁𝑁 relative momenta (𝑝) up to next-to-leading order [NLO] and next-to-next-to-next-to-leading order [N3LO]. We consider two classes of potential: one that acts in all partial waves and another that is dominated by 𝑠-wave physics. The two classes produce broadly similar results for calibrations to 𝑁𝑁 data up to 𝐸_{lab}=5 MeV. Our analysis accounts for the correlated uncertainties that arise from the truncation of the EFT. We simultaneously estimate both the EFT LECs and the EFT breakdown scale, Λ𝑏: the 95% intervals are Λ𝑏 ∈ [50,63] MeV at NLO and Λ𝑏 ∈ [72,88] MeV at N3LO. Invoking naive dimensional analysis for the 𝑁𝑁 potential therefore does not lead to consistent results across orders.
J. M. Bub, M. Piarulli, R. J. Furnstahl, S. Pastore, and D. R. Phillips
Phys. Rev. C 111, 034005 (2025)
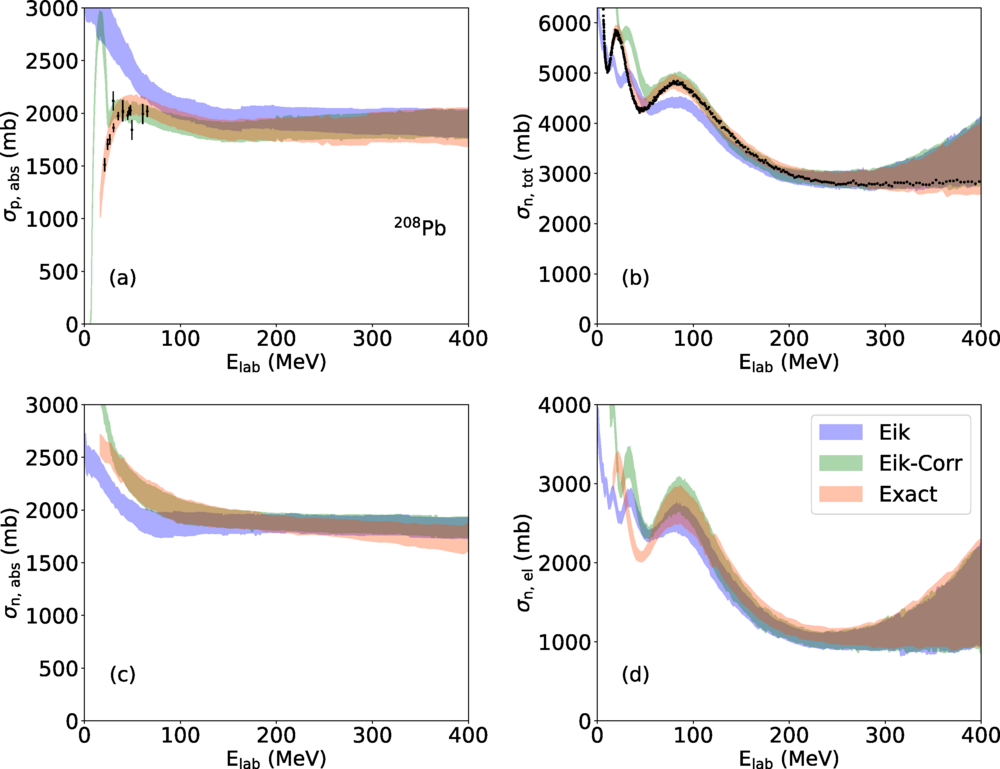
A systematic study of parametric uncertainties in transfer reactions is performed using the recently developed uncertainty quantified global optical potential (KDUQ).
C. Hebborn, F.M. Nunes
Front. Phys. 13, 1525170 (2025)
We perform a systematic study to test the validity of the eikonal approximation for nucleon-nucleus reactions and determine regions of validity for the approximation. We also quantify uncertainties due to the nucleon optical potential on the reaction observables.
D. Shiu, C. Hebborn, and F.M. Nunes
Phys. Rev. C 112, 054609 (2025)
Two different methods, Monte Carlo sampling and variational inference (VI), were used for Bayesian calibration of the effective-range parameters in 3He–4He elastic scattering. The parameters were calibrated to data from a recent 3He–4He elastic scattering differential cross section experiment. Analysis of these data for Elab ≤ 4.3 MeV yields a unimodal posterior for which both methods obtain the same structure. However, the effective-range expansion amplitude does not account for the 7/2− state of 7Be so, even after calibration, the description of data at the upper end of this energy range is poor. The data up to Elab = 2.6 MeV can be well described, but calibration to this lower-energy subset of the data yields a bimodal posterior. After adapting VI to treat such a multi-modal posterior we find good agreement between the VI results and those obtained with parallel-tempered Monte Carlo sampling.
A. Burnelis, V. Kejzlar, D. R. Phillips
Estimating parameters of simulation models based on observed data is an especially challenging task when the computational expense of the model – necessitated by faithfully capturing the real system – limits the learning process. When simulation models are expensive to evaluate, emulators are often built to efficiently approximate model outputs during model calibration. Computing-informed active learning, guided by intelligent acquisition functions, can improve data collection for emulators, thereby enhancing the calibration’s efficiency. However, the performance of active learning strategies depends on computational factors such as computing environment (e.g., parallel resources available), tradeoffs in (calibration and simulation) algorithm’s ability to benefit from parallelism, and the computational expense of the simulation models. In addition to overviewing these considerations, this work provides examples exemplifying the tradeoffs that make such learning difficult.
Özge Sürer, Stefan M. Wild
NeurIPS 2024 Workshop on Bayesian Decision-making and Uncertainty
The equation of state (EOS) in the limit of infinite symmetric nuclear matter exhibits an equilibrium density at which the pressure vanishes and the energy per particle attains its minimum. Although not directly measurable, the nuclear saturation point (𝑛0,𝐸0) can be extrapolated by density-functional theory (DFT), providing tight constraints for microscopic interactions derived from chiral effective-field theory (EFT). We present a Bayesian mixture model that combines multiple DFT predictions for (𝑛0,𝐸0) using an efficient conjugate prior approach. The inferred posterior distribution for the saturation point’s mean and covariance matrix follows a normal-inverse-Wishart (NIW) class, resulting in posterior predictives in the form of correlated, bivariate 𝑡 distributions. The DFT uncertainty reports are then used to mix these posteriors using an ordinary Monte Carlo approach. Our Bayesian framework is publicly available, so practitioners can readily use and extend our results.
C. Drischler, P.G. Giuliani, S. Bezoui, J. Piekarewicz, F. Viens
Physical Review C 110, 044320 (2024)
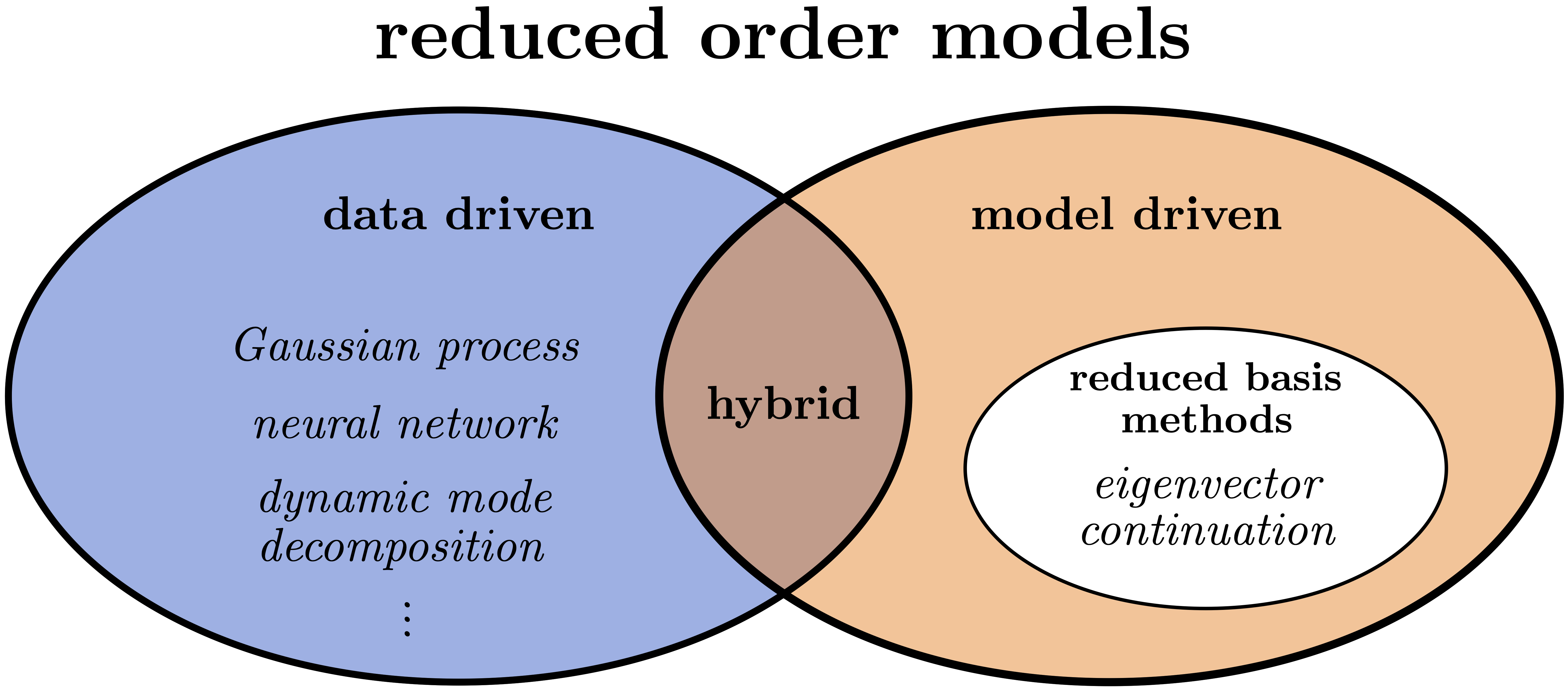
Eigenvector continuation is a computational method for parametric eigenvalue problems that uses subspace projection with a basis derived from eigenvector snapshots from different parameter sets. It is part of a broader class of subspace-projection techniques called reduced-basis methods. In this Colloquium, the development, theory, and applications of eigenvector continuation and projection-based emulators are presented. The basic concepts are introduced, the underlying theory and convergence properties are discussed, and recent applications for quantum systems and future prospects are presented.
T. Duguet, A. Ekström, R.J. Furnstahl, S. König and D. Lee
Reviews of Modern Physics 96, 031002 (2024)
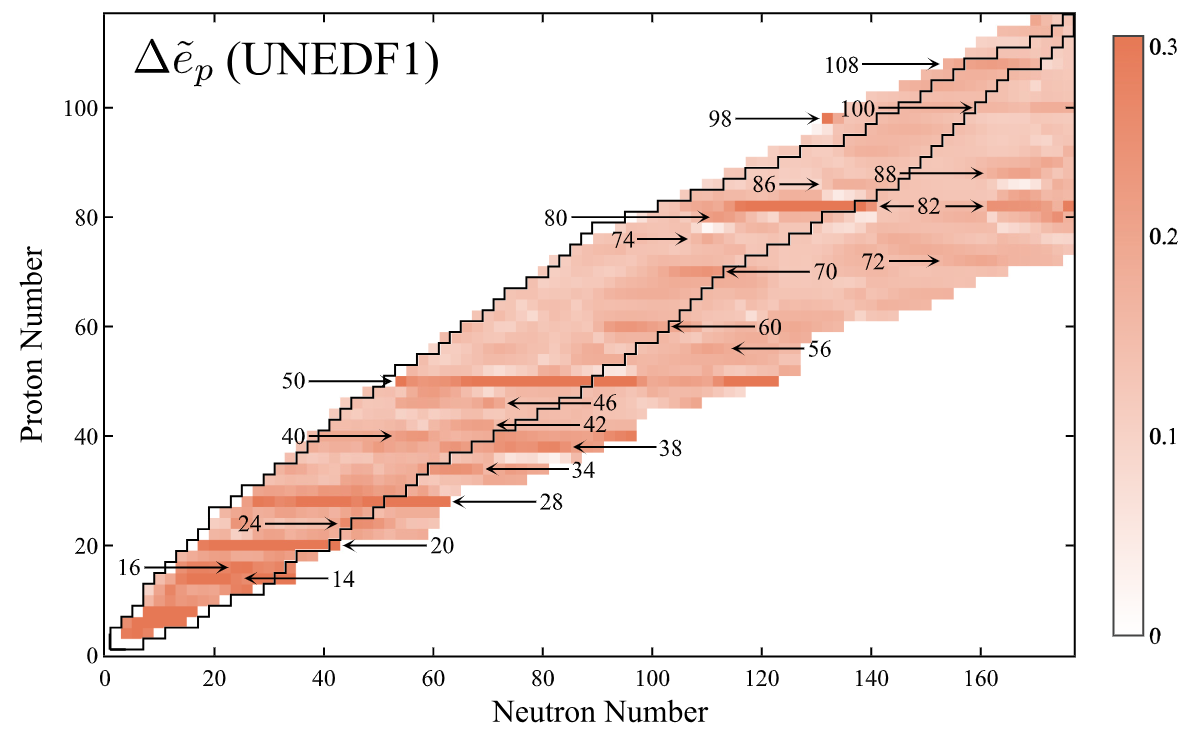
The binding energy of an isotope is a sensitive indicator of the underlying shell structure as it reflects the net energy content of a nucleus. Since magic nuclei are significantly lighter, or more bound, compared to their neighbors, the presence of nucleonic shell structure makes an imprint on nuclear masses. In this work, using a carefully designed binding-energy indicator, we catalog the appearance of spherical and deformed shell and subshell closures throughout the nuclear landscape. After presenting experimental evidence for shell and subshell closures as seen through the lens of nuclear masses, we study the ability of global nuclear mass models to predict local binding-energy variations related to shell effects.
L. Buskirk, K. Godbey, W. Nazarewicz, and W. Satula
Phys. Rev. C 109, 044311 (2024)
We test the BUQEYE model of correlated effective field theory (EFT) truncation errors on Reinert, Krebs, and Epelbaum’s semilocal momentum-space implementation of the chiral EFT (𝜒EFT) expansion of the nucleon-nucleon (NN) potential. This Bayesian model hypothesizes that dimensionless coefficient functions extracted from the order-by-order corrections to NN observables can be treated as draws from a Gaussian process (GP). We combine a variety of graphical and statistical diagnostics to assess when predicted observables have a 𝜒EFT convergence pattern consistent with the hypothesized GP statistical model. All our results can be reproduced using a publicly available Jupyter notebook, which can be straightforwardly modified to analyze other 𝜒EFT NN potentials.
P. J. Millican, R. J. Furnstahl, J. A. Melendez, D. R. Phillips, and M. T. Pratola
Physical Review C 110, 044002 (2024)
Simulation models often have parameters as input and return outputs to understand the behavior of complex systems. Calibration is the process of estimating the values of the parameters in a simulation model in light of observed data from the system that is being simulated. When simulation models are expensive, emulators are built with simulation data as a computationally efficient approximation of an expensive model. An emulator then can be used to predict model outputs, instead of repeatedly running an expensive simulation model during the calibration process. Sequential design with an intelligent selection criterion can guide the process of collecting simulation data to build an emulator, making the calibration process more efficient and effective. This article proposes two novel criteria for sequentially acquiring new simulation data in an active learning setting by considering uncertainties on the posterior density of parameters. Analysis of several simulation experiments and real-data simulation experiments from epidemiology demonstrates that proposed approaches result in improved posterior and field predictions.
Özge Sürer
Journal of Quality Technology (2024)
One can improve predictability in the unknown domain by combining forecasts of imperfect complex computational models using a Bayesian statistical machine learning framework. In many cases, however, the models used in the mixing process are similar. In addition to contaminating the model space, the existence of such similar, or even redundant, models during the multimodeling process can result in misinterpretation of results and deterioration of predictive performance. In this paper we describe a method based on the principal component analysis that eliminates model redundancy. We show that by adding model orthogonalization to the proposed Bayesian model combination framework, one can arrive at better prediction accuracy and reach excellent uncertainty quantification performance.
P. Giuliani, K. Godbey, V. Kejzlar, W. Nazarewicz
Uncertainty quantification using Bayesian methods is a growing area of research. Bayesian model mixing (BMM) is a recent development which combines the predictions from multiple models such that the fidelity of each model is preserved in the final result. Practical tools and analysis suites that facilitate such methods are therefore needed. Taweret1 introduces BMM to existing Bayesian uncertainty quantification efforts. Currently, Taweret contains three individual Bayesian model mixing techniques, each pertaining to a different type of problem structure; we encourage the future inclusion of user-developed mixing methods. Taweret’s first use case is in nuclear physics, but the package has been structured such that it should be adaptable to any research engaged in model comparison or model mixing.
K. Ingles, D. Liyanage, A. C. Semposki, J. C. Yannotty
J. Open Source Softw. 9(97), 6175 (2024)
We revisit the comparison between the frequentist approach and the Bayesian calibration, testing different likelihood assumptions. There is agreement for a simple linear model, but as the complexity of the physics model increase, and the number of parameters gets larger, the Bayesian approach proves to be more robust.
C.D. Pruitt, A.E. Lovell, C. Hebborn, F.M. Nunes
Phys. Rev. C 110, 044311 (2024)
Charge-exchange reactions are versatile probes for nuclear structure. In particular, when populating isobaric analog states, these reactions are used to study isovector nuclear densities and neutron skins. The quality of the information extracted from charge-exchange data depends on the accuracy of the reaction models and their inputs. We quantify the uncertainties due to effective nucleon-nucleus interactions by propagating the parameter posterior distributions of the recent global optical model KDUQ. We also perform a comparison between two- and three-body models that both describe the dynamics of the reaction within the DWBA.
A.J. Smith, C. Hebborn, F.M. Nunes and R. Zegers
Phys. Rev. C 110, 034602 (2024)
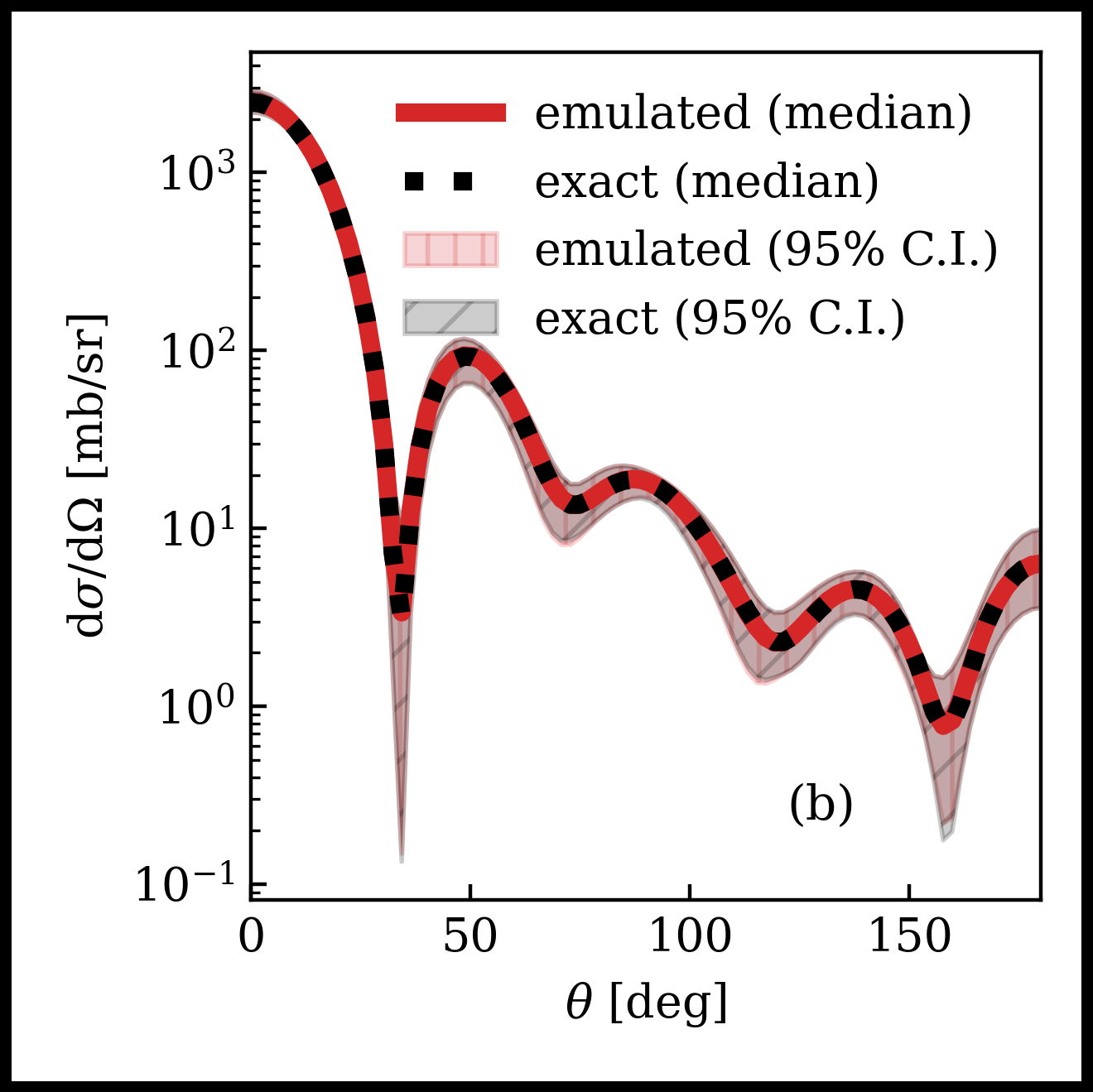
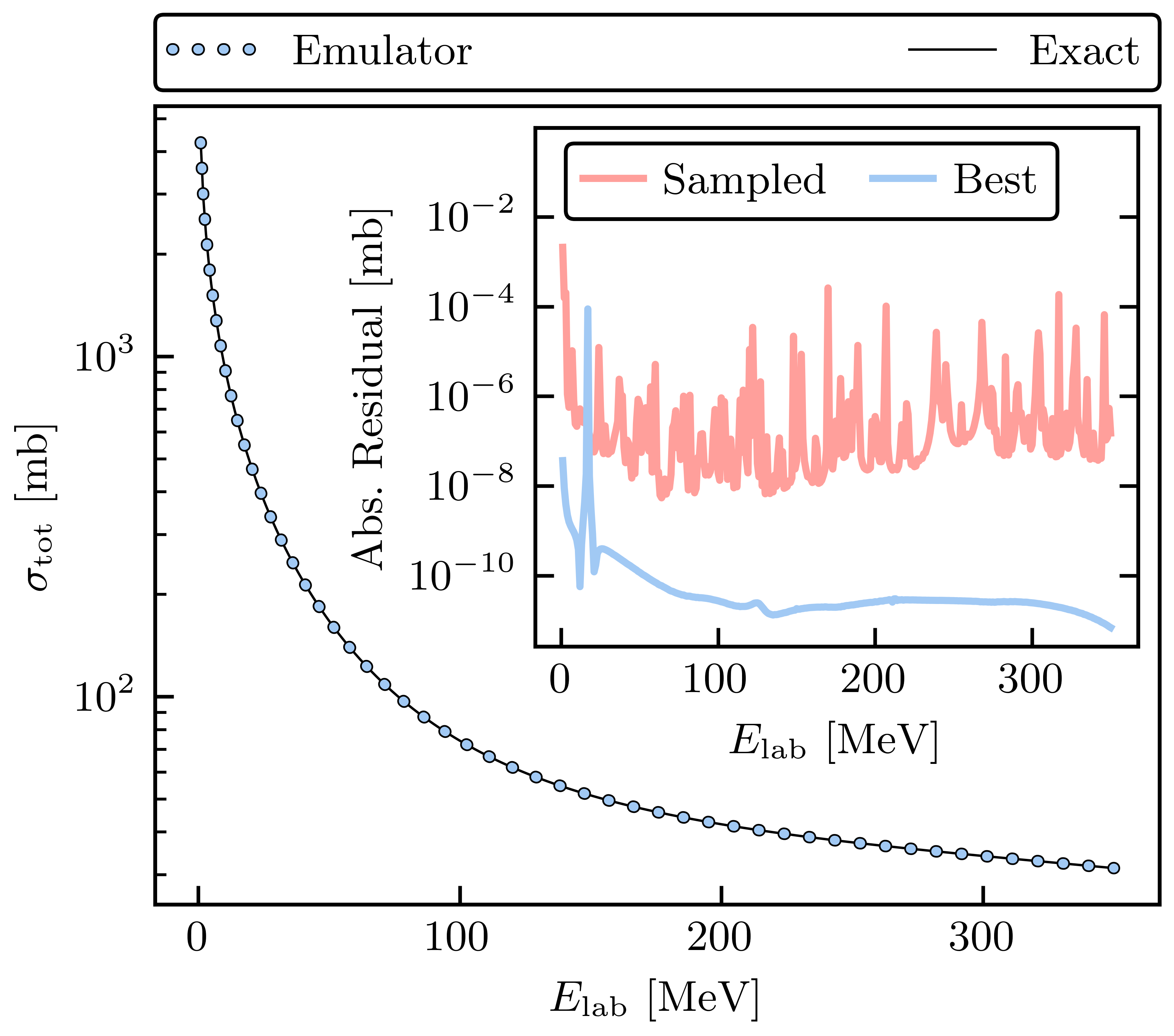
A new generation of phenomenological optical potentials requires robust calibration and uncertainty quantification, motivating the use of Bayesian statistical methods. These Bayesian methods usually require calculating observables for thousands or even millions of parameter sets, making fast and accurate emulators highly desirable or even essential. Emulating scattering across different energies or with interactions such as optical potentials is challenging because of the nonaffine parameter dependence, meaning the parameters do not all factorize from individual operators. Here we introduce and demonstrate the reduced-order scattering emulator (ROSE) framework, a reduced basis emulator that can handle nonaffine problems. ROSE is fully extensible and works within the publicly available BAND framework software suite. As a demonstration problem, we use ROSE to calibrate a realistic nucleon-target scattering model through the calculation of elastic cross sections. This problem shows the practical value of the ROSE framework for Bayesian uncertainty quantification with controlled trade-offs between emulator speed and accuracy as compared to high-fidelity solvers.
D. Odell, P. Giuliani, K. Beyer, M. Catacora-Rios, M. Y.-H. Chan, E. Bonilla, R. J. Furnstahl, K. Godbey, and F. M. Nunes
Physical Review C 109, 044612 (2024)
Decision trees built with data remain in widespread use for nonparametric prediction. Predicting probability distributions is preferred over point predictions when uncertainty plays a prominent role in analysis and decision-making. We study modifying a tree to produce nonparametric predictive distributions. We find the standard method for building trees may not result in good predictive distributions and propose changing the splitting criteria for trees to one based on proper scoring rules. Analysis of both simulated data and several real datasets demonstrates that using these new splitting criteria results in trees with improved predictive properties considering the entire predictive distribution.
Sara Shashaani, Özge Sürer, Matthew Plumlee, and Seth Guikema.
We show the system of a heavy charged particle and a neutral atom can be described by a low-energy effective field theory where the attractive 1/r^4 induced dipole potential determines the long-distance, low-energy wave functions. The 1/r^4 interaction is renormalized by a contact interaction at leading order. Derivative corrections to that contact interaction give rise to higher-order terms. We show that this “induced-dipole EFT” (ID-EFT) reproduces the π+-hydrogen phase shifts of a more microscopic potential, the Temkin-Lamkin potential, over a wide range of energies. Already at leading order it also describes the highest-lying excited bound states of the pionic-hydrogen ion. Lower-lying bound states receive substantial corrections at next-to-leading order, with the size of the correction proportional to their distance from the scattering threshold. Our next-to-leading order calculation show that the three highest-lying bound states of the Temkin-Lamkin potential are well described in ID-EFT.
Daniel Odell, Daniel R. Phillips, and Ubirajara van Kolck
Physical Review C 108, 062817 (2023)
We introduce a flexible Bayesian model mixing methodology using tree basis functions. In modern computer experiment applications, one often encounters the situation where various models of a physical system are considered, each implemented as a simulator on a computer. An important question in such a setting is determining the best simulator, or the best combination of simulators, to use for prediction and inference. Bayesian model averaging (BMA) and stacking are two statistical approaches used to account for model uncertainty by aggregating a set of predictions through a simple linear combination or weighted average, but this ignores the localized behavior of each simulator. This paper proposes a BMM model based on Bayesian Additive Regression Trees (BART) which has the desired flexibility to capture each simulators local behavior. The proposed methodology is applied to combine predictions from Effective Field Theories (EFTs) associated with a motivating nuclear physics application.
J.C. Yannotty, T.J. Santner, R.J. Furnstahl, M.T. Pratola.
Due to large pressure gradients at early times, standard hydrodynamic model simulations of relativistic heavy-ion collisions do not become reliable until O(1)fm/c after the collision. To address this one often introduces a pre-hydrodynamic stage that models the early evolution microscopically, typically as a conformal, weakly interacting gas. In such an approach the transition from the pre-hydrodynamic to the hydrodynamic stage is discontinuous, introducing considerable theoretical model ambiguity. Alternatively, fluids with large anisotropic pressure gradients can be handled macroscopically using the recently developed Viscous Anisotropic Hydrodynamics (VAH). In high-energy heavy-ion collisions VAH is applicable already at very early times, and at later times transitions smoothly into conventional second-order viscous hydrodynamics (VH). We present a Bayesian calibration of the VAH model with experimental data for Pb–Pb collisions at the LHC. We find that the VAH model has the unique capability of constraining the specific viscosities of the QGP at higher temperatures than other previously used models.
D. Liyanage, Ö. Sürer, M. Plumlee, S.M. Wild, U. Heinz.
Physical Review C 108, 054905 (2023)
To improve the predictability of complex computational models in experimentally-unknown domains, we propose a Bayesian statistical machine learning framework that uses the Dirichlet distribution to combine results of several imperfect models. This framework can be viewed as an extension of Bayesian stacking. To illustrate the method, we study the ability of Bayesian model averaging and mixing techniques to mine nuclear masses. We show that the global and local mixtures of models reach excellent performance on both prediction accuracy and uncertainty quantification and are preferable to classical Bayesian model averaging. Additionally, our statistical analysis indicates that improving model predictions through mixing rather than mixing of corrected models leads to more robust extrapolations.
Vojta Kejzlar, Leo Neufcourt, and Witek Nazarewicz
Scientific Reports 13, 19600 (2023)
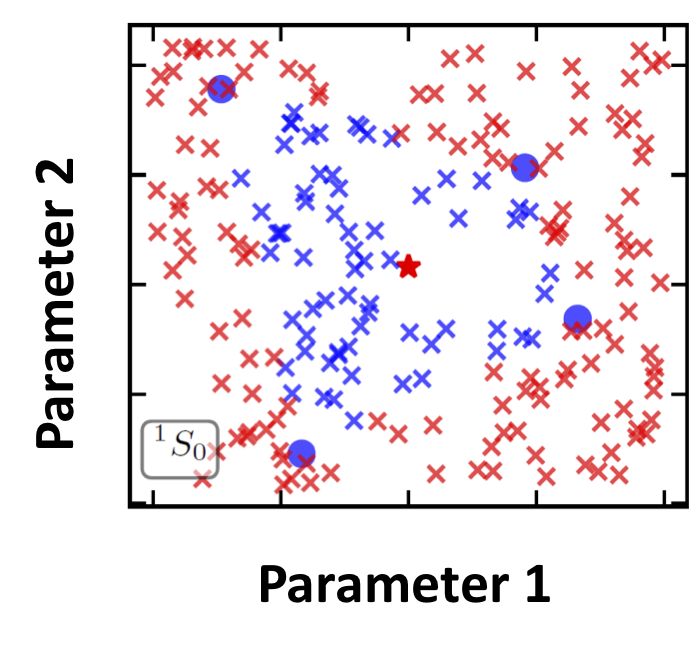
Simulation models of critical systems often have parameters that need to be calibrated using observed data. For expensive simulation models, calibration is done using an emulator of the simulation model built on simulation output at different parameter settings. Using intelligent and adaptive selection of parameters to build the emulator can drastically improve the efficiency of the calibration process. The article proposes a sequential framework with a novel criterion for parameter selection that targets learning the posterior density of the parameters. The emergent behavior from this criterion is that exploration happens by selecting parameters in uncertain posterior regions while simultaneously exploitation happens by selecting parameters in regions of high posterior density. The advantages of the proposed method are illustrated using several simulation experiments and a nuclear physics reaction model.
Özge Sürer, Matthew Plumlee, and Stefan M. Wild.
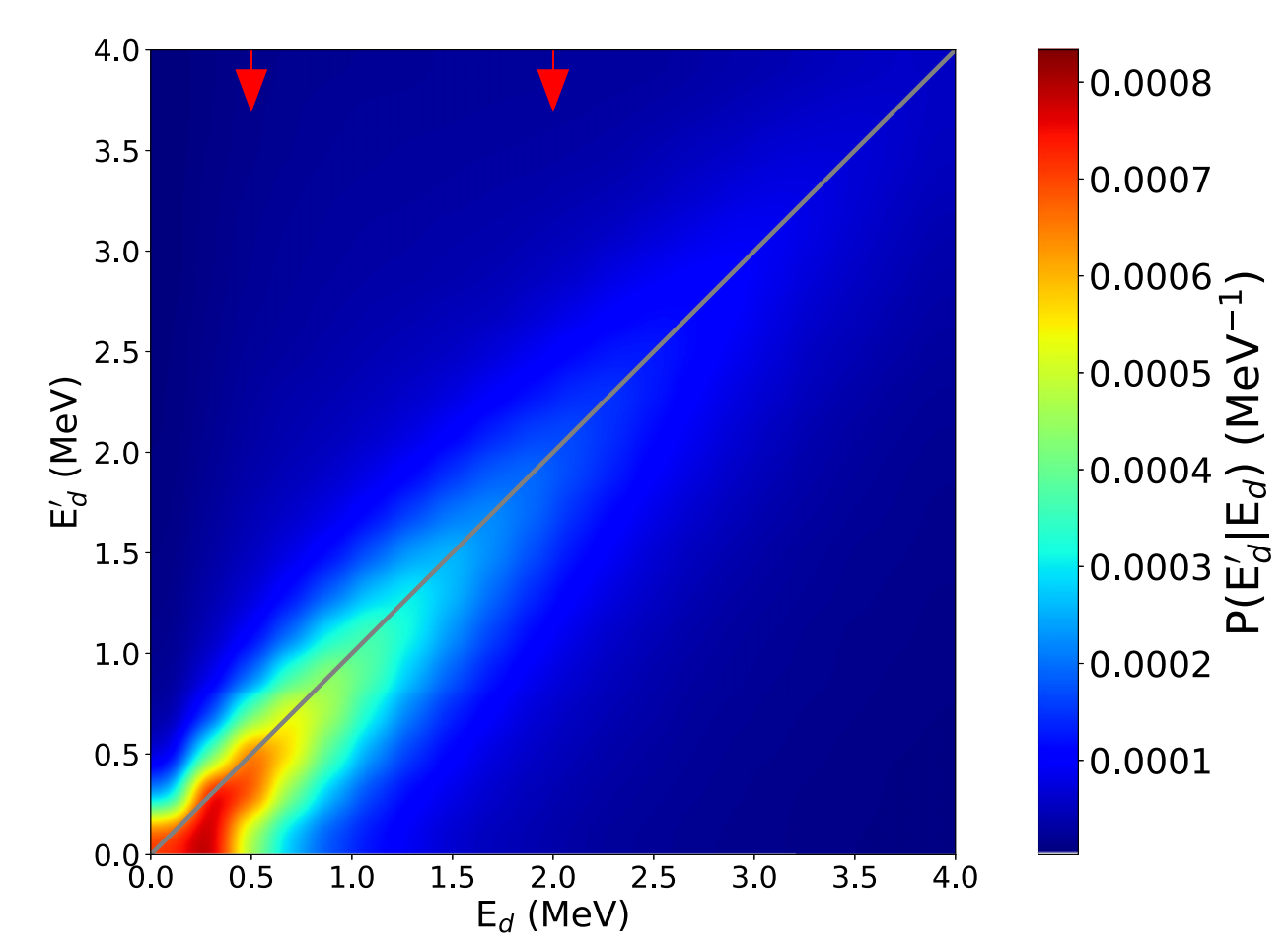
In nuclear reaction experiments, the measured decay energy spectra can give insights into the shell structure of decaying systems. However, extracting the underlying physics from the measurements is challenging due to detector resolution and acceptance effects. The Richardson-Lucy (RL) algorithm, a deblurring method that is commonly used in optics, was applied to our experimental nuclear physics data. The only inputs to the method are the observed energy spectrum and the detector’s response matrix. We demonstrate that the technique can help access information about the shell structure of particle-unbound systems from the measured decay energy spectrum that is not immediately accessible via traditional approaches such as χ-square fitting. For a similar purpose, we developed a deep neural network (DNN) classifier to identify resonance states from the measured decay energy spectrum. We tested the performance of both methods on simulated data and experimental measurements. Then, we applied both algorithms to the decay energy spectrum of 26O→24O+n+n measured via invariant mass spectroscopy. The resonance states restored using the RL algorithm to deblur the measured decay energy spectrum agree with those found by the DNN classifier. Both approaches suggest that the raw decay energy spectrum of 26O exhibits three peaks at approximately 0.15 MeV, 1.50 MeV, and 5.00 MeV, with half-widths of 0.29 MeV, 0.80 MeV, and 1.85 MeV, respectively.
Pierre Nzabahimana, Thomas Redpath, Thomas Baumann, Pawel Danielewicz, Pablo Giuliani, and Paul Guèye
Gaussian process surrogates are a popular alternative to directly using computationally expensive simulation models. When the simulation output consists of many responses, dimension-reduction techniques are often employed to construct these surrogates. However, surrogate methods with dimension reduction generally rely on complete output training data. This article proposes a new Gaussian process surrogate method that permits the use of partially observed output while remaining computationally efficient. The new method involves the imputation of missing values and the adjustment of the covariance matrix used for Gaussian process inference. The resulting surrogate represents the available responses, disregards the missing responses, and provides meaningful uncertainty quantification. The proposed approach is shown to offer sharper inference than alternatives in a simulation study and a case study where an energy density functional model that frequently returns incomplete output is calibrated.
Moses Y-H. Chan, Matthew Plumlee, and Stefan M. Wild.
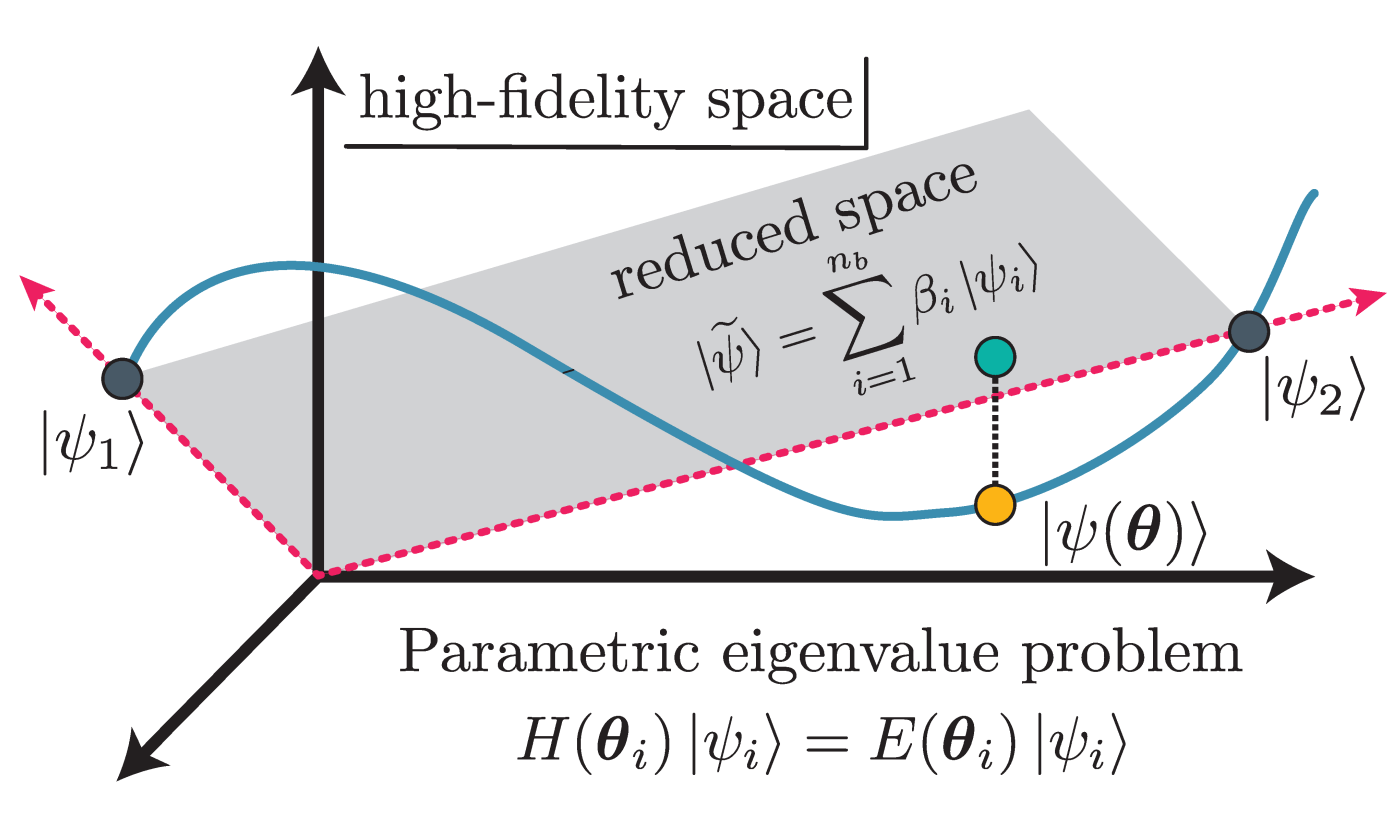
The BUQEYE collaboration (Bayesian Uncertainty Quantification: Errors in Your effective field theory) presents a pedagogical introduction to projection-based, reduced-order emulators for applications in low-energy nuclear physics. The term emulator refers here to a fast surrogate model capable of reliably approximating high-fidelity models. As the general tools employed by these emulators are not yet well-known in the nuclear physics community, we discuss variational and Galerkin projection methods, emphasize the benefits of offline-online decompositions, and explore how these concepts lead to emulators for bound and scattering systems that enable fast and accurate calculations using many different model parameter sets. We also point to future extensions and applications of these emulators for nuclear physics, guided by the mature field of model (order) reduction. All examples discussed here and more are available as interactive, open-source Python code so that practitioners can readily adapt projection-based emulators for their own work.
Christian Drischler, Jordan Melendez, Dick Furnstahl, Alberto Garcia, and Xilin Zhang.
Front. Phys. 10, 1092931 (2023)
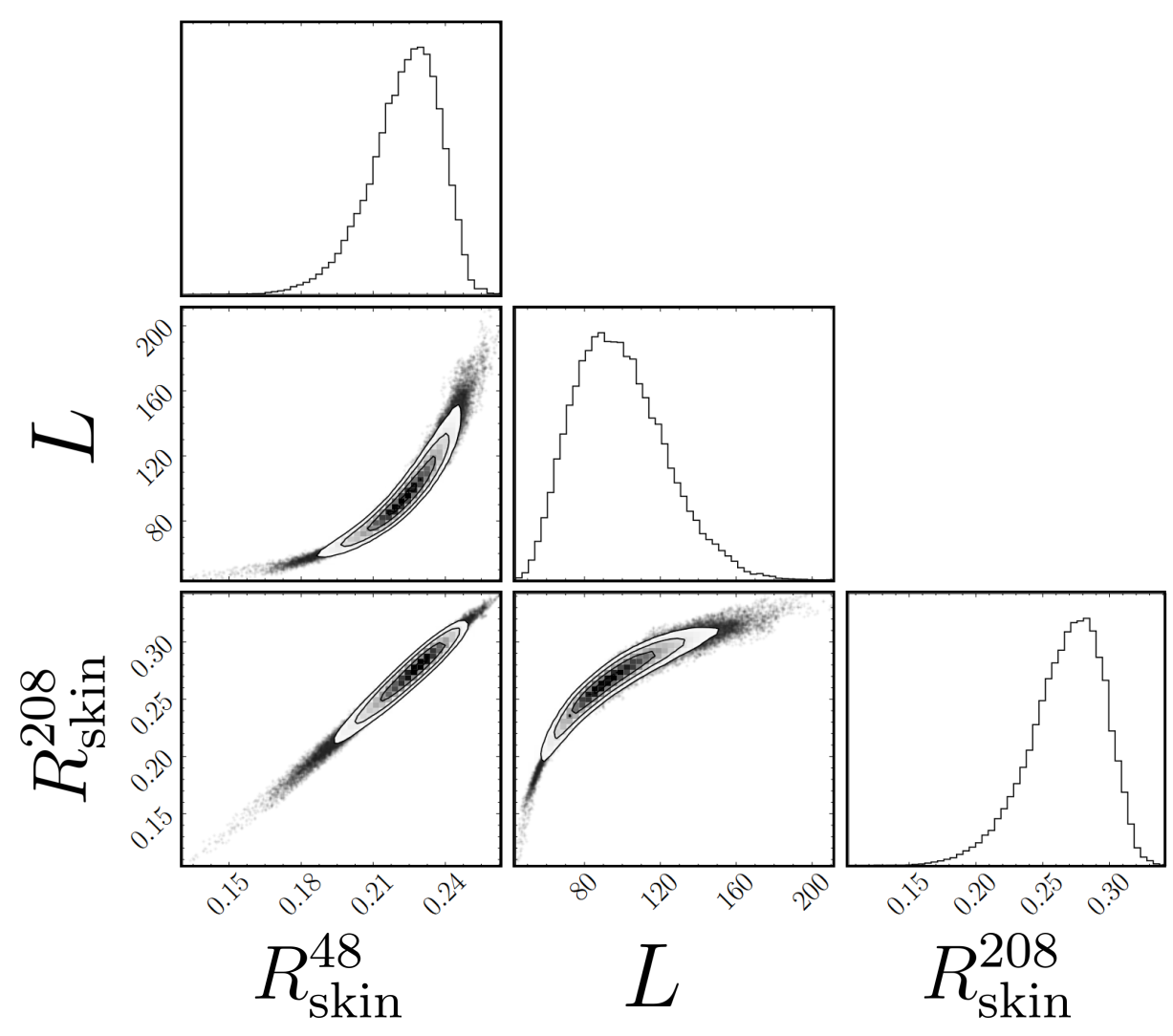
A covariant energy density functional is calibrated using a principled Bayesian statistical framework informed by experimental binding energies and charge radii of several magic and semi-magic nuclei. The Bayesian sampling required for the calibration is enabled by the emulation of the high-fidelity model through the implementation of a reduced basis method (RBM)—a set of dimensionality reduction techniques that can speed up demanding calculations involving partial differential equations by several orders of magnitude. The RBM emulator is able to accurately reproduce the model calculations in tens of milliseconds on a personal computer, an increase in speed of nearly a factor of 3,300. Besides the analysis of the posterior distribution of parameters, we present model calculations for masses and radii with properly estimated uncertainties. We also analyze the model correlation between the slope of the symmetry energy L and the neutron skin of 48Ca and 208Pb.
Pablo Giuliani, Kyle Godbey, Edgard Bonilla, Frederi Viens, and Jorge Piekarewicz.
Front. Phys. 10, 1054524 (2023)
ParMOO is a Python framework and library of solver components for building and deploying highly customized multiobjective simulation optimization solvers. ParMOO is designed to help engineers, practitioners, and optimization experts exploit available structures in how simulation outputs are used to formulate the objectives for a multiobjective optimization problem.
T.H. Chang and S.M. Wild
J. Open Source Softw. 8(82), 4468 (2023)
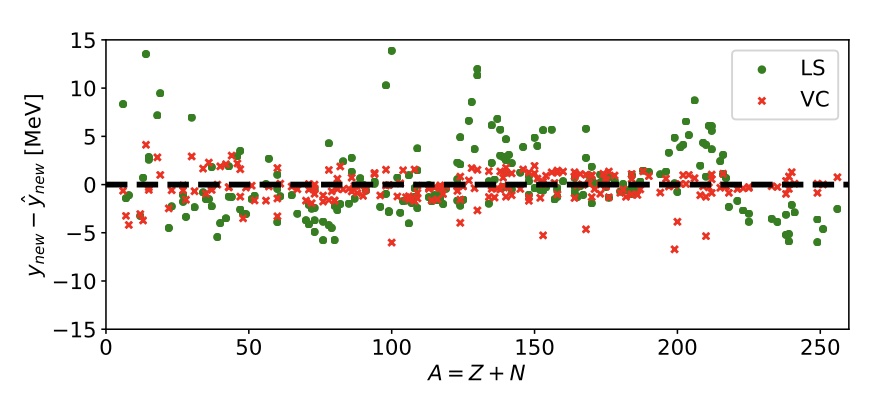
With the advancements of computer architectures, the use of computational models proliferates to solve complex problems in many scientific applications such as nuclear physics and climate research. However, the potential of such models is often hindered because they tend to be computationally expensive. We develop a computationally efficient algorithm based on variational Bayes inference (VBI) for calibration of computer models with Gaussian processes. Unfortunately, the standard fast-to-compute gradient estimates based on subsampling are biased under the calibration framework due to the conditionally dependent data which diminishes the efficiency of VBI. In this work, we adopt a pairwise decomposition of the data likelihood using vine copulas that separate the information on dependence structure in data from their marginal distributions and leads to computationally efficient gradient estimates that are unbiased and thus scalable calibration. We provide empirical evidence for the computational scalability of our methodology together with average case analysis and all the necessary details for an efficient implementation of the proposed algorithm. We also demonstrate the opportunities given by our method for practitioners on a real data example through calibration of the Liquid Drop Model of nuclear binding energies.
V. Kejzlar and T. Maiti
Statistics and Computing 33, 18 (2022)
Proposed mechanisms for the production of calcium in the first stars that formed out of the matter of the Big Bang are at odds with observations. Advanced nuclear burning and supernovae were thought to be the dominant source of the calcium production seen in all stars. Here we suggest a qualitatively different path to calcium production: breakout from the ‘warm’ carbon–nitrogen–oxygen (CNO) cycle. We report a direct experimental measurement of the 19F(p, γ)20Ne breakout reaction down to a very low energy of 186 kiloelectronvolts, and characterize a key resonance at 225 kiloelectronvolts. For temperatures of astrophysical interest–around 0.1 gigakelvin–this thermonuclear 19F(p, γ)20Ne rate is roughly a factor of seven larger than the previously recommended one. Our stellar models show a stronger breakout during stellar hydrogen burning than previously thought and may reveal the nature of calcium production in population III stars imprinted on the oldest known ultra-iron-poor star, SMSS0313-67086. This experimental result was obtained in the China JinPing Underground Laboratory7, which offers an environment with an extremely low cosmic-ray-induced background. Our rate showcases the effect that faint population III star supernovae can have on the nucleosynthesis observed in the oldest known stars and first galaxies, which are key mission targets of the James Webb Space Telescope.
L. Zhang,…, D. Odell et al.
Nature volume 610, pages 656–660 (2022)
We present the reduced basis method as a tool for developing emulators for equations with tunable parameters within the context of the nuclear many-body problem. The method uses a basis expansion informed by a set of solutions for a few values of the model parameters and then projects the equations over a well-chosen low-dimensional subspace. We connect some of the results in the eigenvector continuation literature to the formalism of reduced basis methods and show how these methods can be applied to a broad set of problems. As we illustrate, the possible success of the formalism on such problems can be diagnosed beforehand by a principal component analysis. We apply the reduced basis method to the one-dimensional Gross-Pitaevskii equation with a harmonic trapping potential and to nuclear density functional theory for 48Ca, achieving speed-ups of more than ×150 and ×250, respectively, when compared to traditional solvers. The outstanding performance of the approach, together with its straightforward implementation, show promise for its application to the emulation of computationally demanding calculations, including uncertainty quantification.
Edgard Bonilla, Pablo Giuliani, Kyle Godbey, and Dean Lee.
Phys. Rev. C 106, 054322 (2022)
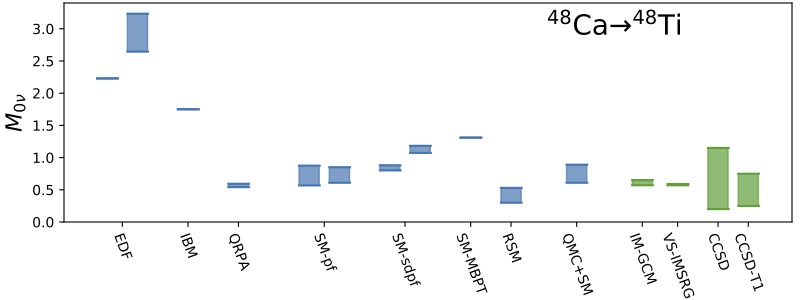
We present the results of a National Science Foundation Project Scoping Workshop, the purpose of which was to assess the current status of calculations for the nuclear matrix elements governing neutrinoless double-beta decay and determine if more work on them is required. After reviewing important recent progress in the application of effective field theory, lattice quantum chromodynamics, and ab initio nuclear-structure theory to double-beta decay, we discuss the state of the art in nuclear-physics uncertainty quantification and then construct a roadmap for work in all these areas to fully complement the increasingly sensitive experiments in operation and under development. The roadmap includes specific projects in theoretical and computational physics as well as the use of Bayesian methods to quantify both intra- and inter-model uncertainties. The goal of this ambitious program is a set of accurate and precise matrix elements, in all nuclei of interest to experimentalists, delivered together with carefully assessed uncertainties. Such calculations will allow crisp conclusions from the observation or non-observation of neutrinoless double-beta decay, no matter what new physics is at play.
V. Cirigliano, Z. Davoudi, J. Engel, R. J. Furnstahl, G. Hagen, U. Heinz, and 17 other authors, including W. Nazarewicz, D. R. Phillips, M. Plumlee, F. Viens, and S. M. Wild.
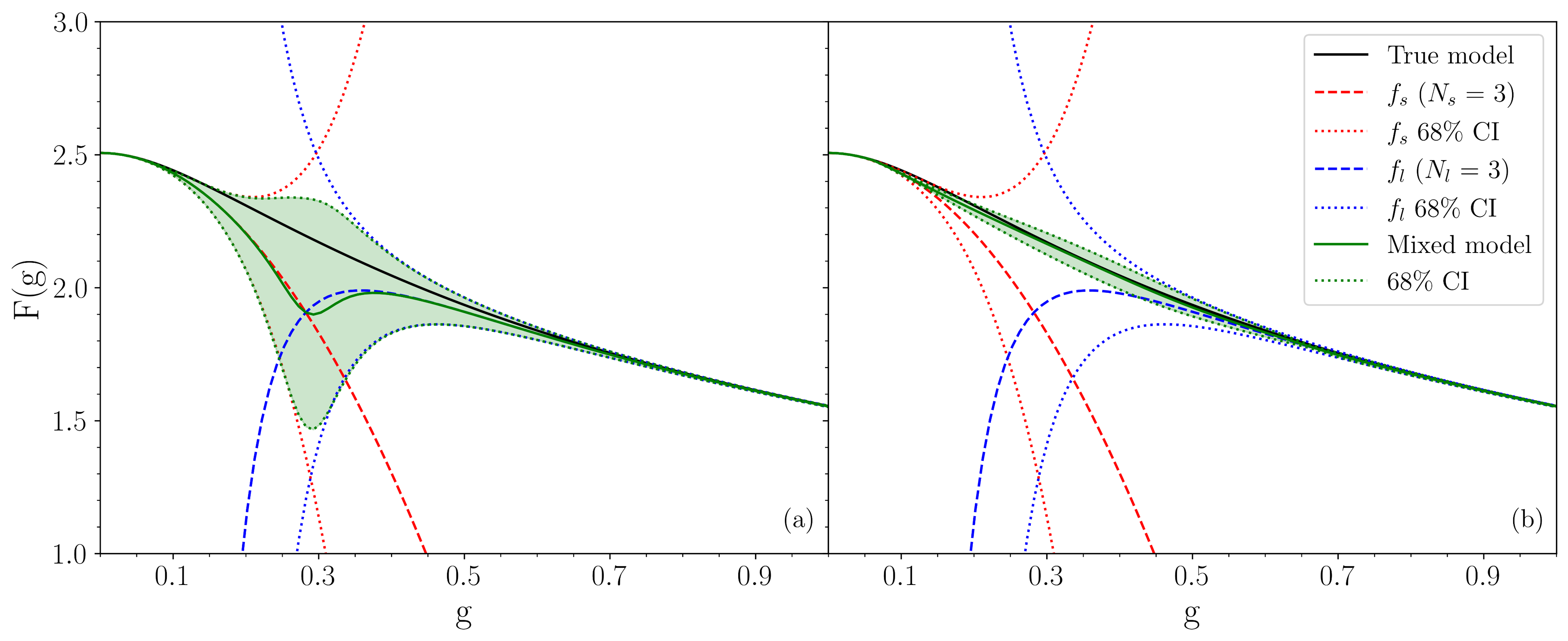
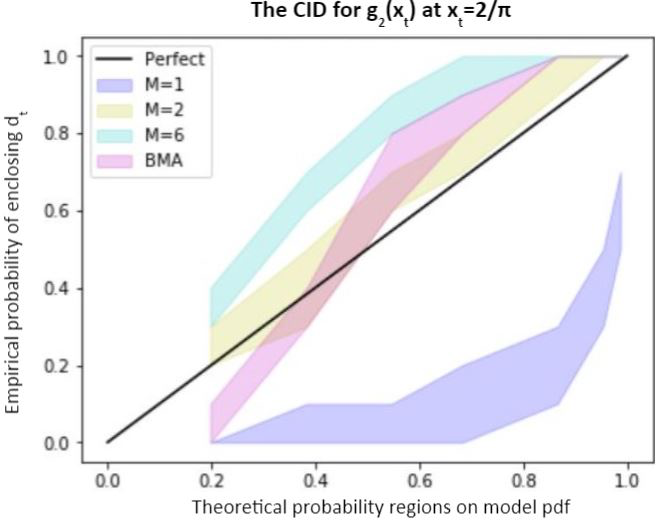
Bayesian model mixing (BMM) is a statistical technique that can be used to combine models that are predictive in different input domains into a composite distribution that has improved predictive power over the entire input space. We explore the application of BMM to the mixing of two expansions of a function of a coupling constant g that are valid at small and large values of g respectively. This type of problem is quite common in nuclear physics, where physical properties are straightforwardly calculable in strong and weak interaction limits or at low and high densities or momentum transfers, but difficult to calculate in between. Interpolation between these limits is often accomplished by a suitable interpolating function, e.g., Padé approximants, but it is then unclear how to quantify the uncertainty of the interpolant. We address this problem in the simple context of the partition function of zero-dimensional $\phi^4$ theory, for which the (asymptotic) expansion at small g and the (convergent) expansion at large g are both known. We consider three mixing methods: linear mixture BMM, localized bivariate BMM, and localized multivariate BMM with Gaussian processes. We find that employing a Gaussian process in the intermediate region between the two predictive models leads to the best results of the three methods. The methods and validation strategies we present here should be generalizable to other nuclear physics settings.
A. C. Semposki, R. J. Furnstahl, D. R. Phillips
Phys. Rev. C 106, 044002 (2022)
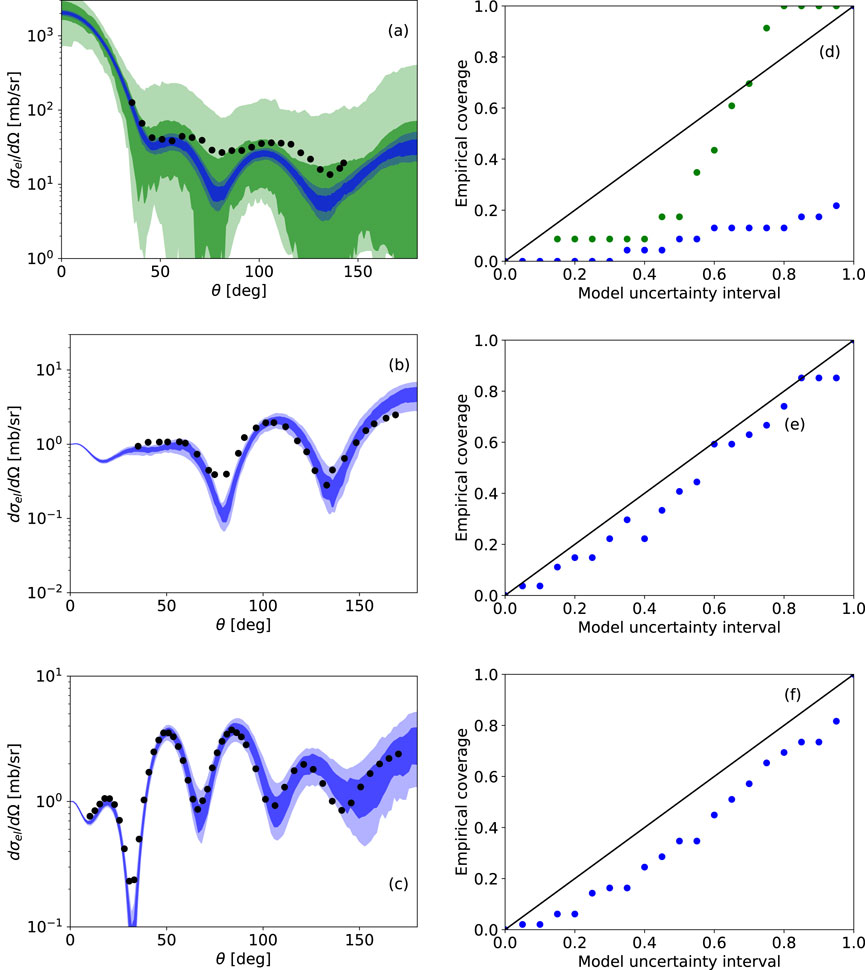
Breakup reactions are one of the favored probes to study loosely bound nuclei near the limits of stability. In order to interpret such breakup experiments, the continuum discretized coupled channel method is typically used. In this study, the first Bayesian analysis of a breakup reaction model is performed. We use a combination of statistical methods together with a three-body reaction model to quantify the uncertainties on the breakup observables due to the parameters in the effective potential describing the loosely bound projectile of interest. The combination of tools we develop opens the path for a Bayesian analysis of a wide array of complex nuclear processes that require computationally intensive reaction models.
O. Surer, F. M. Nunes, M. Plumlee, S. M. Wild
Phys. Rev. C 106, 024607 (2022)
The field of model order reduction (MOR) is growing in importance due to its ability to extract the key insights from complex simulations while discarding computationally burdensome and superfluous information. We provide an overview of MOR methods for the creation of fast & accurate emulators of memory- and compute-intensive nuclear systems, focusing on eigen-emulators and variational emulators. As an example, we describe how ‘eigenvector continuation’ is a special case of a much more general and well-studied MOR formalism for parameterized systems. We continue with an introduction to the Ritz and Galerkin projection methods that underpin many such emulators, while pointing to the relevant MOR theory and its successful applications along the way. We believe that this guide will open the door to broader applications in nuclear physics and facilitate communication with practitioners in other fields.
J. A. Melendez, C. Drischler, R. J. Furnstahl, A. J. Garcia, Xilin Zhang
We use a recently developed Effective Field Theory (EFT) for rotational bands in odd-mass nuclei to perform a Bayesian analysis of energy-level data in several nuclei. The error model in our Bayesian analysis includes both experimental and EFT truncation uncertainties. It also accounts for the fact that low-energy constants (LECs) at even and odd orders have different sizes. We use Markov Chain Monte Carlo sampling to explore the joint posterior of the EFT and error-model parameters and show both can be reliably determined. We extract the LECs up to fourth order in the EFT and find that, provided we correctly account for EFT truncation errors, results for lower-order LECs are stable as we go to higher orders. LEC results are also stable with respect to the addition of higher-energy data. We find a clear correlation between the extracted and the expected value of the inverse breakdown scale. The EFT turns out to converge markedly better than would be naively expected based on the scales of the problem
I.K. Alnamlah, E.A. Coello Pérez, D.R. Phillips
Front. in Phys. 10, 901954 (2022)
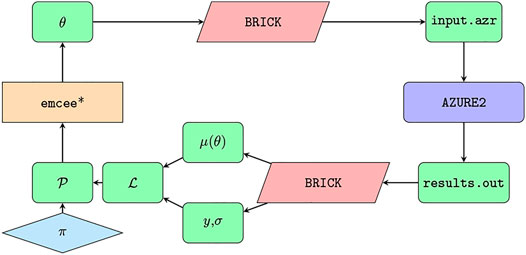
Phenomenological R-matrix has been a standard framework for the evaluation of resolved resonance cross section data in nuclear physics for many years. It is a powerful method for comparing different types of experimental nuclear data and combining the results of many different experimental measurements in order to gain a better estimation of the true underlying cross sections. Yet a practical challenge has always been the estimation of the uncertainty on both the cross sections at the energies of interest and the fit parameters, which can take the form of standard level parameters. In this work, the emcee Markov Chain Monte Carlo sampler has been implemented for the R-matrix code AZURE2, creating the Bayesian R-matrix Inference Code Kit (BRICK). Bayesian uncertainty estimation has then been carried out for a simultaneous R-matrix fit of a capture and scattering reaction in the 7Be system.
D. Odell, C. R. Brune, D. R. Phillips, R. J. deBoer, S. N. Paneru
Front. in Phys. 10, 888746 (2022)
Advances in machine learning methods provide tools that have broad applicability in scientific research. These techniques are being applied across the diversity of nuclear physics research topics, leading to advances that will facilitate scientific discoveries and societal applications. This Colloquium provides a snapshot of nuclear physics research, which has been transformed by machine learning techniques.
A. Boehnlein, M. Diefenthaler, C. Fanelli, M. Hjorth-Jensen, T. Horn, M. P. Kuchera, D. Lee, W. Nazarewicz, K. Orginos, P. Ostroumov, L.-G. Pang, A. Poon, N. Sato, M. Schram, A. Scheinker, M. S. Smith,X.-N. Wang, V. Ziegler
Rev. Mod. Phys. 94, 031003 (2022)
We develop a class of emulators for solving quantum three-body scattering problems based on combining the variational method for scattering observables and eigenvector continuation. The emulators are first trained by the exact scattering solutions for a small number of parameter sets, and then employed to make interpolations and extrapolations in the parameter space. Using a schematic nuclear-physics model with finite-range two and three-body interactions, we demonstrate the emulators to be extremely accurate and efficient. The general strategies used here may be applicable for building the same type of emulators in other fields, wherever variational methods can be developed for evaluating physical models.
Xilin Zhang and R. J. Furnstahl
Phys. Rev. C 105, 064004 (2022)
The statistical correlations between nuclear deformations and charge radii of different nuclei are affected by the underlying shell structure. Even for well deformed and superfluid nuclei for which these observables change smoothly, the correlation range is rather short. This result suggests that the frequently made assumption of reduced statistical errors for the differences between smoothly-varying observables cannot be generally justified.
Paul-Gerhard Reinhard and Witold Nazarewicz
Phys. Rev. C 106, 014303 (2022)
State-of-the-art hydrodynamic models of heavy-ion collisions have considerable theoretical model uncertainties in the description of the very early pre-hydrodynamic stage. We add a new computational module, KTIso, that describes the pre-hydrodynamic evolution kinetically, based on the relativistic Boltzmann equation with collisions treated in the Isotropization Time Approximation. As a novelty, KTIso allows for the inclusion and evolution of initial-state momentum anisotropies. To maintain computational efficiency KTIso assumes strict longitudinal boost invariance and allows collisions to isotropize only the transverse momenta. We use it to explore the sensitivity of hadronic observables measured in relativistic heavy-ion collisions to initial-state momentum anisotropies and microscopic scattering during the pre-hydrodynamic stage.
D. Liyanage, D. Everett, C. Chattopadhyay, U. Heinz
Pnys. Rev. C 105, 064908 (2022)
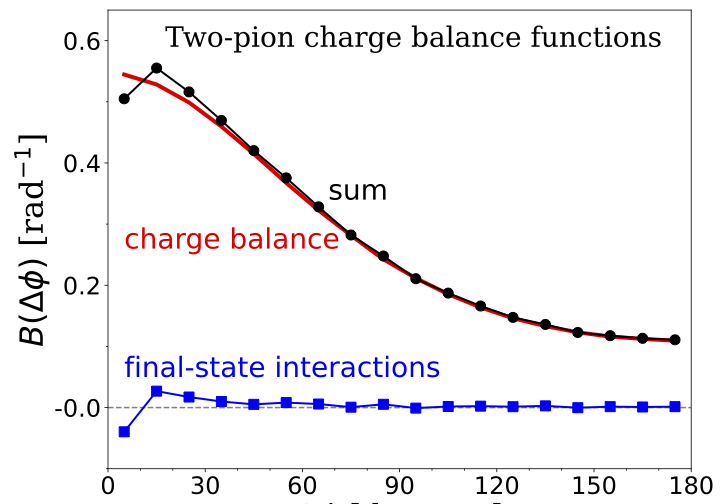
Correlations driven by the constraints of local charge conservationprovide insight into the chemical evolution and diffusivity of the high-temperature matter created in ultra-relativistic heavy ion collisions. Two-particle correlations driven by final-state interactions have allowed the extraction of critical femtoscopic space-time information about the expansion and dissolution of the same collisions. As first steps toward a Bayesian analysis of charge-balance functions, this study quantifies the contribution from final-state interactions, which needs to be subtracted in order to quantitatively infer the diffusivity and chemical evolution of the QGP. As seen in the figure, the correction from final-state interactions is small.
Scott Pratt and Karina Martirosova
Phys. Rev. C 105, 054906 (2022)
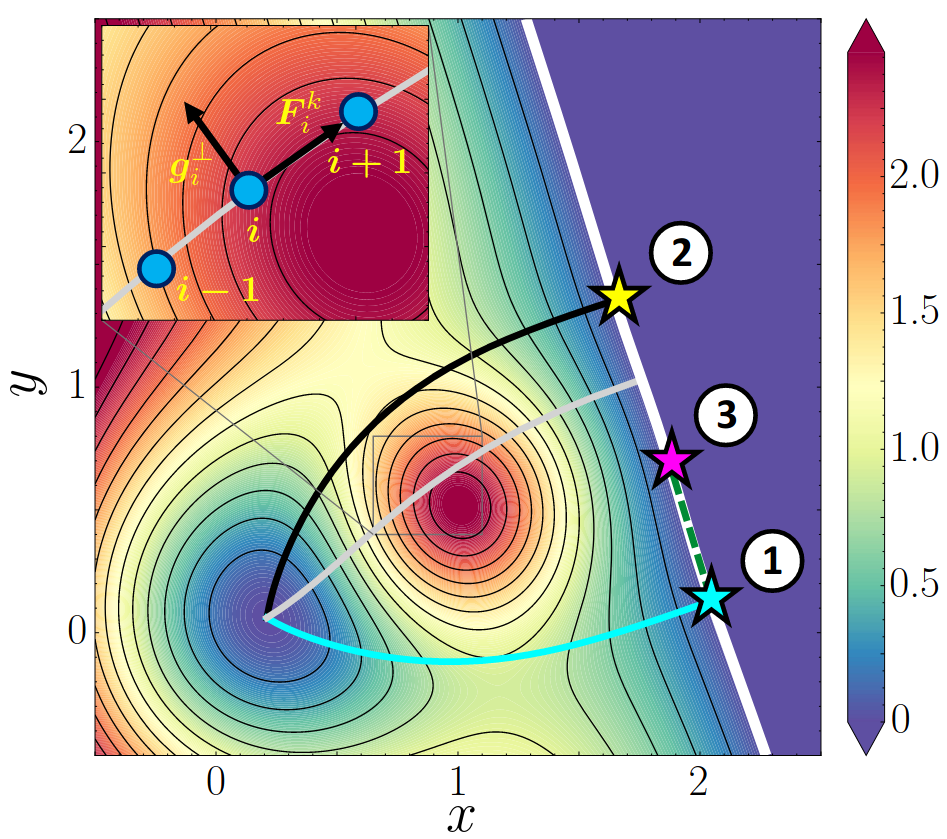
The nuclear fission process is a dramatic example of the large-amplitude collective motion in which the nucleus undergoes a series of shape changes before splitting into distinct fragments. This motion can be represented by a pathway in the many-dimensional space of collective coordinates. Within a stationary framework rooted in a static collective Schrödinger equation, the collective action along the fission pathway determines the spontaneous fission half-lives as well as mass and charge distributions of fission fragments. We study the performance and precision of various methods to determine the minimum-action and minimum-energy fission trajectories in two- and three-dimensional collective spaces. These methods include the nudged elastic band method (NEB), grid-based methods, and the Euler-Lagrange approach to the collective action minimization. The NEB method is capable of efficient determination of the exit points on the outer turning surface that characterize the most probable fission pathway and constitute the key input for fission studies. The NEB method will be particularly useful in large-scale static fission calculations of superheavy nuclei and neutron-rich fissioning nuclei contributing to the astrophysical r-process recycling.
Eric Flynn, Daniel Lay, Sylvester Agbemava, Pablo Giuliani, Kyle Godbey, Witold Nazarewicz, Jhilam Sadhukhan
Phys. Rev. C 105, 054302 (2022)
We treat low-energy 3He-alpha elastic scattering in an Effective Field Theory (EFT) that exploits the separation of scales in this reaction. We compute the amplitude up to Next-to-Next-to-Leading Order (NNLO), developing a hierarchy of the effective-range parameters that contribute at various orders. We use the resulting formalism to analyze data for recent measurements at center-of-mass energies of 0.38-3.12 MeV using the SONIK gas target at TRIUMF as well as older data in this energy regime. We employ a likelihood function that incorporates the theoretical uncertainty due to truncation of the EFT and use Markov Chain Monte Carlo sampling to obtain the resulting posterior probability distribution. We find that the inclusion of a small amount of data on the analysing power $A_y$ is crucial to determine the sign of the p-wave splitting in such an analysis. The combination of Ay and SONIK data constrains all effective-range parameters up to O(p^4) in both s- and p-waves quite well. The ANCs and s-wave scattering length are consistent with a recent EFT analysis of the capture reaction 3He(alpha,gamma)7Be.
M. Poudel, D. R. Phillips
For many decades now, Bayesian Model Averaging (BMA) has been a popular framework to systematically account for model uncertainty that arises in situations when multiple competing models are available to describe the same or similar physical process. The implementation of this framework, however, comes with a multitude of practical challenges including posterior approximation via Markov Chain Monte Carlo and numerical integration. We present a Variational Bayesian Inference approach to BMA as a viable alternative to the standard solutions which avoids many of the aforementioned pitfalls. The proposed method is “black box” in the sense that it can be readily applied to many models with little to no model-specific derivation. We illustrate the utility of our variational approach on a suite of examples and discuss all the necessary implementation details. Fully documented Python code with all the examples is provided as well.
V. Kejzlar, S. Bhattacharya, M. Son, T. Maiti
The American Statistician (2022)
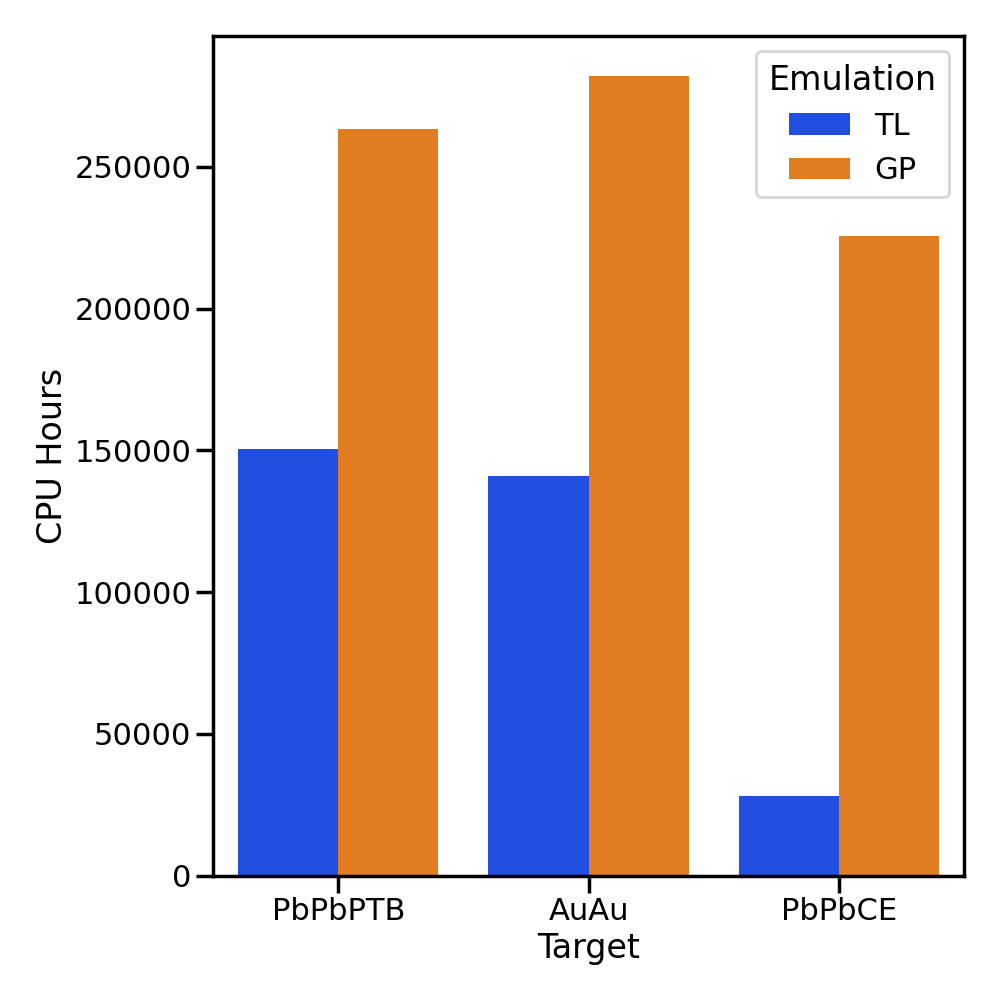
Measurements from the Large Hadron Collider (LHC) and the Relativistic Heavy Ion Collider (RHIC) can be used to study the properties of quark-gluon plasma. Systematic constraints on these properties must combine measurements from different collision systems and methodically account for experimental and theoretical uncertainties. Such studies require a vast number of costly numerical simulations. While computationally inexpensive surrogate models (“emulators”) can be used to efficiently approximate the predictions of heavy ion simulations across a broad range of model parameters, training a reliable emulator remains a computationally expensive task. We use transfer learning to map the parameter dependencies of one model emulator onto another, leveraging similarities between different simulations of heavy ion collisions. By limiting the need for large numbers of simulations to only one of the emulators, this technique reduces the numerical cost of comprehensive uncertainty quantification when studying multiple collision systems and exploring different models.
D. Liyanage, Y. Ji, D. Everett, M. Heffernan, U. Heinz, S. Mak, J-F. Paquet
Physical Review C 105, 034910 (2022)
Modern statistical tools provide the ability to compare the information content of observables and provide a path to explore which experiments would be most useful to give insight into and constrain theoretical models. In this work we study three such tools, (i) the principal component analysis, (ii) the sensitivity analysis based on derivatives, and (iii) the Bayesian evidence. This is done in the context of nuclear reactions with the goal of constraining the optical potential. We first apply these tools to a toy-model case. Then we consider two different reaction observables, elastic angular distributions and polarization data for reactions on 48Ca and 208Pb at two different beam energies. For the toy-model case, we find significant discrimination power in the sensitivities and the Bayesian evidence, showing clearly that the volume imaginary term is more useful to describe scattering at higher energies. When comparing between elastic cross sections and polarization data using realistic optical models, sensitivity studies indicate that both observables are roughly equally sensitive but the variability of the optical model parameters is strongly angle dependent. The Bayesian evidence shows some variability between the two observables, but the Bayes factor obtained is not sufficient to discriminate between angular distributions and polarization.
M. Catacora-Rios, G. B. King, A. E. Lovell, and F. M. Nunes
Physical Review C 104, 064611 (2021)
We explore the constraints on the three-nucleon force (3NF) of chiral effective field theory (ChiEFT) that are provided by bound-state observables in the A=3 and A=4 sectors. Our statistically rigorous analysis incorporates experimental error, computational method uncertainty, and the uncertainty due to truncation of the ChiEFT expansion at next-to-next-to-leading order. A consistent solution for the 3H binding energy, the 4He binding energy and radius, and the 3H beta-decay rate can only be obtained if ChiEFT truncation errors are included in the analysis. The beta-decay rate is the only one of these that yields a nondegenerate constraint on the 3NF low-energy constants, which makes it crucial for the parameter estimation. We use eigenvector continuation for fast and accurate emulation of no-core shell model calculations of the few-nucleon observables. This facilitates sampling of the posterior probability distribution, allowing us to also determine the distributions of the parameters that quantify the truncation error. We find a ChiEFT expansion parameter of Q=0.33 ± 0.06 for these observables.
S. Wesolowski, I. Svensson, A. Ekström, C. Forssén, R. J. Furnstahl, J. A. Melendez, and D. R. Phillips
Physical Review C 104, 064001 (2021)
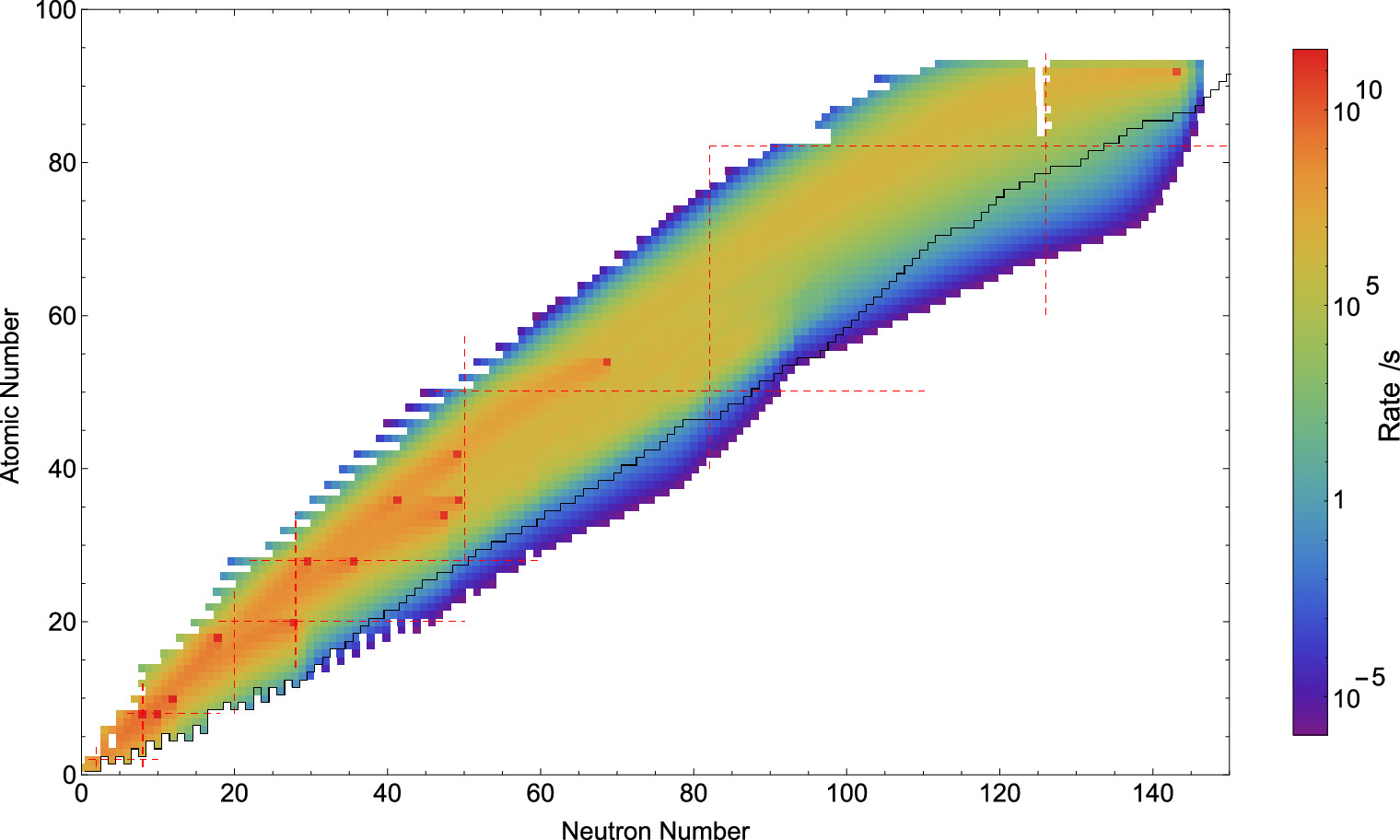
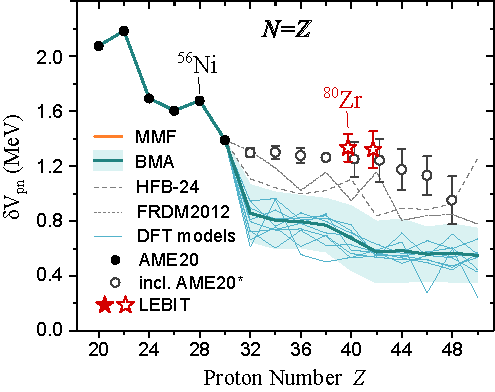
Protons and neutrons in the atomic nucleus move in shells analogous to the electronic shell structures of atoms. The nuclear shell structure varies as a result of changes in the nuclear mean field with the number of neutrons N and protons Z, and these variations can be probed by measuring the mass differences between nuclei. The N = Z = 40 self-conjugate nucleus 80Zr is of particular interest, as its proton and neutron shell structures are expected to be very similar, and its ground state is highly deformed. Here we provide evidence for the existence of a deformed double-shell closure in 80Zr through high-precision Penning trap mass measurements of 80–83Zr. Our mass values show that 80Zr is substantially lighter, and thus more strongly bound than predicted. This can be attributed to the deformed shell closure at N = Z = 40 and the large Wigner energy. A statistical Bayesian-model mixing analysis employing several global nuclear mass models demonstrates difficulties with reproducing the observed mass anomaly using current theory.
A. Hamaker, E. Leistenschneider, R. Jain, G. Bollen, S. A. Giuliani, K. Lund, W. Nazarewicz, L. Neufcourt, C. R. Nicoloff, D. Puentes, R. Ringle, C. S. Sumithrarachchi, and I. T. Yandow
We construct an efficient emulator for two-body scattering observables using the general (complex) Kohn variational principle and trial wave functions derived from eigenvector continuation. The emulator simultaneously evaluates an array of Kohn variational principles associated with different boundary conditions, which allows for the detection and removal of spurious singularities known as Kohn anomalies. When applied to the K-matrix only, our emulator resembles the one constructed by Furnstahl et al. (2020) although with reduced numerical noise. After a few applications to real potentials, we emulate differential cross sections for 40Ca(n,n) scattering based on a realistic optical potential and quantify the model uncertainties using Bayesian methods. These calculations serve as a proof of principle for future studies aimed at improving optical models.
C. Drischler, M. Quinonez, P.G. Giuliani, A.E. Lovell, and F.M. Nunes
Physics Letters B 823, 136777 (2021)
We assess the accuracy of Bayesian polynomial extrapolations from small parameter values to large ones. We employ Bayesian Model Averaging (BMA) to combine results from different order polynomials. Our study considers two “toy problems” where the underlying function used to generate data sets is known. We use Bayesian parameter estimation to extract the polynomial coefficients and BMA different polynomial degrees by weighting each according to its Bayesian evidence. We compare the predictive performance of this Bayesian Model Average with that of the individual polynomials.
M. A. Connell, I. Billig, and D. R. Phillips
Eigenvector continuation (EC), which accurately and efficiently reproduces ground states for targeted sets of Hamiltonian parameters, is extended to scattering using the Kohn variational principle. Proofs-of-principle imply EC will be a valuable emulator for applying Bayesian inference to parameter estimation constrained by scattering observables.
R.J. Furnstahl, A.J. Garcia, P.J. Millican, and Xilin Zhang
Physics Letters B 809, 135719 (2020)
We combine Newton’s variational method with ideas from eigenvector continuation to construct a fast & accurate emulator for two-body scattering observables. The emulator will facilitate the application of rigorous statistical methods for interactions that depend smoothly on a set of free parameters. When used to emulate the neutron-proton cross section with a modern chiral interaction as a function of 26 free parameters, it reproduces the exact calculation with negligible error and provides an over 300x improvement in CPU time.
J.A. Melendez, C. Drischler, A.J. Garcia, R.J. Furnstahl, and Xilin Zhang
Physics Letters B 821, 136608 (2021)
A microscopic description of the interaction of atomic nuclei with external electroweak probes is required for elucidating aspects of short-range nuclear dynamics and for the correct interpretation of neutrino oscillation experiments. Nuclear quantum Monte Carlo methods infer the nuclear electroweak response functions from their Laplace transforms. Inverting the Laplace transform is a notoriously ill-posed problem; and Bayesian techniques, such as maximum entropy, are typically used to reconstruct the original response functions in the quasielastic region. In this work, we present a physics-informed artificial neural network architecture suitable for approximating the inverse of the Laplace transform. Utilizing simulated, albeit realistic, electromagnetic response functions, we show that this physics-informed artificial neural network outperforms maximum entropy in both the low-energy transfer and the quasielastic regions, thereby allowing for robust calculations of electron scattering and neutrino scattering on nuclei and inclusive muon capture rates.
K. Raghavan, P. Balaprakash, A. Lovato, N. Rocco, and S.M. Wild
Phys. Rev. C 103, 035502 (2021)
All BAND Publications
Get on the BAND Wagon: A Bayesian Framework for Quantifying Model Uncertainties in Nuclear Dynamics
D.R. Phillips, R.J. Furnstahl, U. Heinz, T. Maiti, W. Nazarewicz, F.M. Nunes, M. Plumlee, M.T. Pratola, S. Pratt, F.G. Viens, and S.M. Wild
J. Phys. G 48, 072001 (2021)
Phenomenological constraints on QCD transport with quantified theory uncertainties
Sunil Jaiswal
Phys. Lett. B 874, 140243 (2026)
Microscopic constraints for the equation of state and structure of neutron stars: A Bayesian model mixing framework
Alexandra C. Semposki, Christian Drischler, Richard J. Furnstahl, Daniel R. Phillips
Phys. Rev. C 113, 015808 (2026)
A new database website for nuclear level densities
Chirag Rathi, Alexander Voinov, Kyle Godbey, Zach Meisel, Kristen Leibensperger
Computer Physics Communications 321 (2026) 110018
Surrogate models for linear response
Lauren Jin, Ante Ravlic, Pablo Giuliani, Kyle Godbey, Witold Nazarewicz
Phys. Rev. Research 7, 043347 (2025)
Bayesian model-data comparison incorporating theoretical uncertainties
Sunil Jaiswal, Chun Shen, Richard J. Furnstahl, Ulrich Heinz, Matthew T. Pratola.
Phys. Lett. B 870, 139946 (2025)
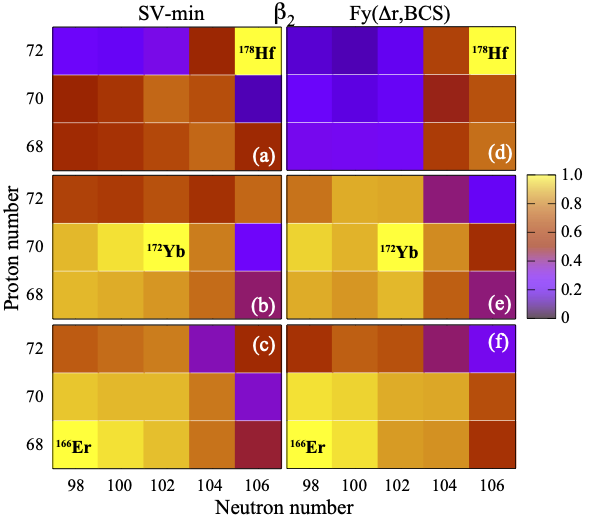
Extraction of ground-state nuclear deformations from ultrarelativistic heavy-ion collisions: Nuclear structure physics context
J. Dobaczewski, A. Gade, K. Godbey, R. V. F. Janssens, and W. Nazarewicz
Phys. Rev. Research 7, 043159 (2025)
Emulators for Scarce and Noisy Data: Application to Auxiliary-Field Diffusion Monte Carlo for Neutron Matter
Cassandra L. Armstrong, Pablo Giuliani, Kyle Godbey, Rahul Somasundaram, and Ingo Tews.
Phys. Rev. Lett. 135, 142501 (2025)
Emulators for scarce and noisy data: Application to auxiliary field diffusion Monte Carlo for the deuteron
Rahul Somasundaram, Cassandra L. Armstrong, Pablo Giuliani, Kyle Godbey, Stefano Gandolfi, and Ingo Tews.
Phys. Lett. B 866, 139558 (2025)
Motivations for early high-profile FRIB experiments
B. Alex Brown, Alexandra Gade, S. Ragnar Stroberg, Jutta E. Escher, Kevin Fossez, Pablo Giuliani, Calem R. Hoffman, Witold Nazarewicz, et al.
J. Phys. G Nucl. Part. Phys. 52 050501 (2025)
Batch sequential experimental design for calibration of stochastic simulation models
Özge Sürer.
Technometrics (2025)
From chiral EFT to perturbative QCD: A Bayesian model mixing approach to symmetric nuclear matter
A. C. Semposki, C. Drischler, R. J. Furnstahl, J. A. Melendez, D. R. Phillips
Phys. Rev. C 111, 035804 (2025)
Bayesian analysis of nucleon-nucleon scattering data in pionless effective field theory
J. M. Bub, M. Piarulli, R. J. Furnstahl, S. Pastore, and D. R. Phillips
Phys. Rev. C 111, 034005 (2025)
Systematic study of the propagation of uncertainties to transfer observables
C. Hebborn, F.M. Nunes
Front. Phys. 13, 1525170 (2025)
Systematic study of the validity of the eikonal model including uncertainties
D. Shiu, C. Hebborn, and F.M. Nunes
Phys. Rev. C 112, 054609 (2025)
Variational inference of effective range parameters for 3He−4He scattering
A. Burnelis, V. Kejzlar, D. R. Phillips
J. Phys. G 52, 015109 (2025)
An active learning performance model for parallel Bayesian calibration of expensive simulations
Özge Sürer, Stefan M. Wild
NeurIPS 2024 Workshop on Bayesian Decision-making and Uncertainty
Bayesian mixture model approach to quantifying the empirical nuclear saturation point
C. Drischler, P.G. Giuliani, S. Bezoui, J. Piekarewicz, F. Viens
Physical Review C 110, 044320 (2024)
Colloquium: Eigenvector continuation and projection-based emulators
T. Duguet, A. Ekström, R.J. Furnstahl, S. König and D. Lee
Reviews of Modern Physics 96, 031002 (2024)
Nucleonic shells and nuclear masses
L. Buskirk, K. Godbey, W. Nazarewicz, and W. Satula
Phys. Rev. C 109, 044311 (2024)
Assessing correlated truncation errors in modern nucleon-nucleon potentials
P. J. Millican, R. J. Furnstahl, J. A. Melendez, D. R. Phillips, and M. T. Pratola
Physical Review C 110, 044002 (2024)
Simulation experiment design for calibration via active learning
Özge Sürer
Journal of Quality Technology (2024)
Model orthogonalization and Bayesian forecast mixing via principal component analysis
P. Giuliani, K. Godbey, V. Kejzlar, W. Nazarewicz
Phys. Rev. R 6, 033266 (2024)
Taweret: a Python package for Bayesian model mixing
K. Ingles, D. Liyanage, A. C. Semposki, J. C. Yannotty
J. Open Source Softw. 9(97), 6175 (2024)
Role of the likelihood for elastic scattering uncertainty quantification
C.D. Pruitt, A.E. Lovell, C. Hebborn, F.M. Nunes
Phys. Rev. C 110, 044311 (2024)
Uncertainty quantification in (p,n) reactions
A.J. Smith, C. Hebborn, F.M. Nunes and R. Zegers
Phys. Rev. C 110, 034602 (2024)
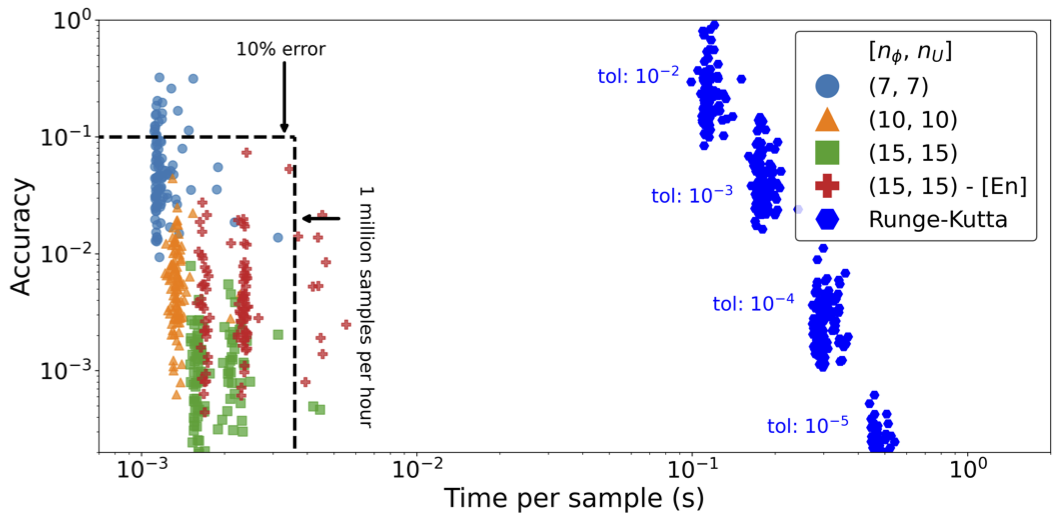
ROSE: A reduced-order scattering emulator for optical models
D. Odell, P. Giuliani, K. Beyer, M. Catacora-Rios, M. Y.-H. Chan, E. Bonilla, R. J. Furnstahl, K. Godbey, and F. M. Nunes
Physical Review C 109, 044612 (2024)
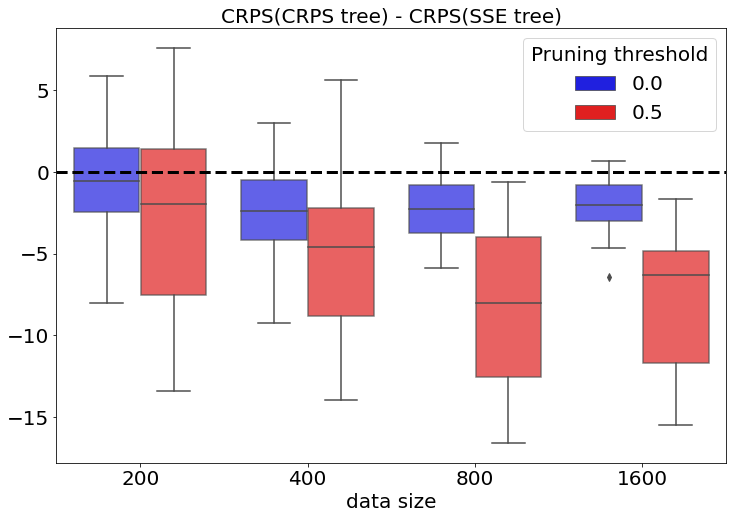
Building trees for probabilistic prediction via scoring rules
Sara Shashaani, Özge Sürer, Matthew Plumlee, and Seth Guikema.
Technometrics (2024)
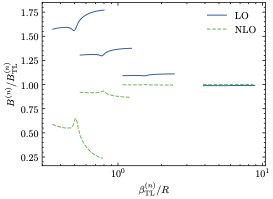
Effective field theory for the bound states and scattering of a heavy charged particle and a neutral atom
Daniel Odell, Daniel R. Phillips, and Ubirajara van Kolck
Physical Review C 108, 062817 (2023)
Absolute cross section of the 12C(p,γ)13N reaction
K-U. Kettner, H. W. Becker, C. R. Brune, R. J. deBoer, J. Görres, D. Odell, D. Rogalla, and M. Wiescher
Physical Review C 108, 035805 (2023)
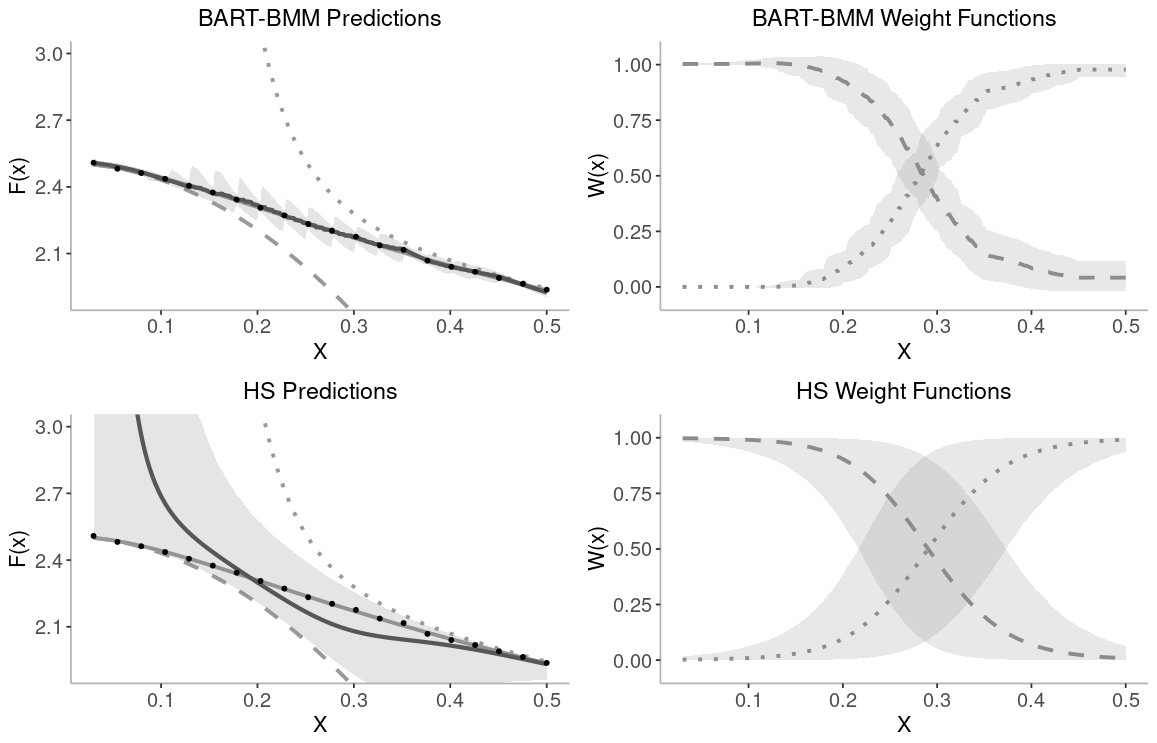
Model Mixing Using Bayesian Additive Regression Trees
J.C. Yannotty, T.J. Santner, R.J. Furnstahl, M.T. Pratola.
Technometrics (2023)
Bayesian calibration of viscous anisotropic hydrodynamic simulations of heavy-ion collisions
D. Liyanage, Ö. Sürer, M. Plumlee, S.M. Wild, U. Heinz.
Physical Review C 108, 054905 (2023)
Local Bayesian Dirichlet mixing of imperfect models
Vojta Kejzlar, Leo Neufcourt, and Witek Nazarewicz
Scientific Reports 13, 19600 (2023)
Sequential Bayesian experimental design for calibration of expensive simulation models
Özge Sürer, Matthew Plumlee, and Stefan M. Wild.
Technometrics (2023)
Deconvoluting experimental decay energy spectra: The 26O case
Pierre Nzabahimana, Thomas Redpath, Thomas Baumann, Pawel Danielewicz, Pablo Giuliani, and Paul Guèye
Phys.Rev.C 107, 064315 (2023)
Constructing a simulation surrogate with partially observed output
Moses Y-H. Chan, Matthew Plumlee, and Stefan M. Wild.
Technometrics (2023)
BUQEYE guide to projection-based emulators in nuclear physics
Christian Drischler, Jordan Melendez, Dick Furnstahl, Alberto Garcia, and Xilin Zhang.
Front. Phys. 10, 1092931 (2023)
Bayes goes fast: Uncertainty quantification for a covariant energy density functional emulated by the reduced basis method
Pablo Giuliani, Kyle Godbey, Edgard Bonilla, Frederi Viens, and Jorge Piekarewicz.
Front. Phys. 10, 1054524 (2023)
ParMOO: A Python library for parallel multiobjective simulation optimization
T.H. Chang and S.M. Wild
J. Open Source Softw. 8(82), 4468 (2023)
Variational inference with vine copulas: an efficient approach for Bayesian computer model calibration
V. Kejzlar and T. Maiti
Statistics and Computing 33, 18 (2022)
First near-threshold measurements of the 13C(α,n1)16O reaction for low-background-environment characterization
R. J. deBoer,…, D. Odell et al.
Phys.Rev.C 106, 055808 (2022)
Direct measurement of the astrophysical 19F(p,αγ)16O reaction in a deep-underground laboratory
L. Zhang,…, D. Odell et al.
Phys.Rev.C 106 (2022)
Measurement of 19F(p, γ)20Ne reaction suggests CNO breakout in first stars
L. Zhang,…, D. Odell et al.
Nature volume 610, pages 656–660 (2022)
Investigation of direct capture in the 23Na(p,γ)24Mg reaction
A. Boeltzig,…, D.Odell et al.
Phys. Rev. C 106, 045801 (2022)
Investigation of the 10B(p,α)7Be reaction from 0.8 to 2.0 MeV
B. Vande Kolk,…, D. Odell et al.
Phys. Rev. C 105, 055802 (2022)
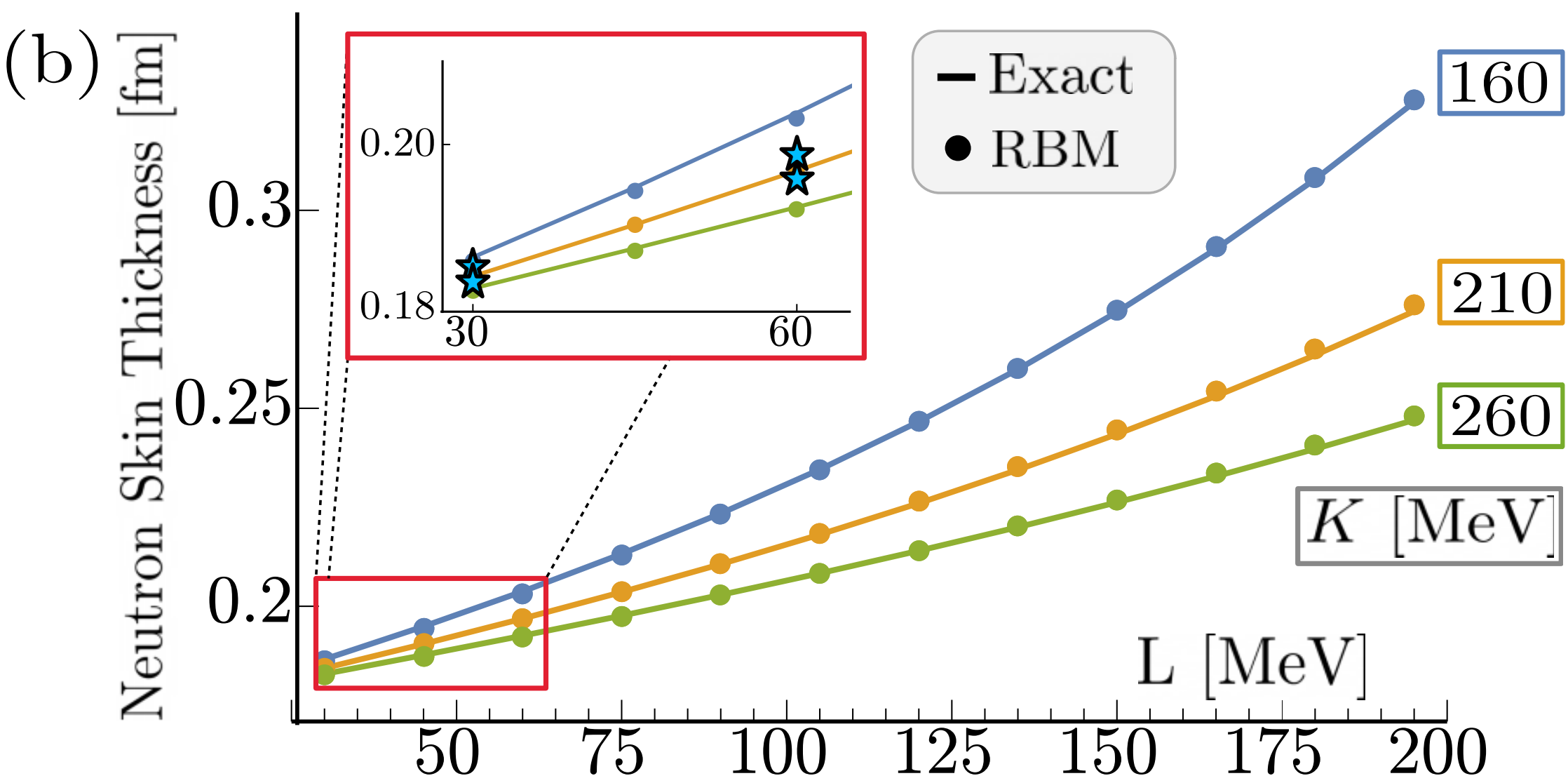
Training and projecting: A reduced basis method emulator for many-body physics
Edgard Bonilla, Pablo Giuliani, Kyle Godbey, and Dean Lee.
Phys. Rev. C 106, 054322 (2022)
Towards precise and accurate calculations of neutrinoless double-beta decay
V. Cirigliano, Z. Davoudi, J. Engel, R. J. Furnstahl, G. Hagen, U. Heinz, and 17 other authors, including W. Nazarewicz, D. R. Phillips, M. Plumlee, F. Viens, and S. M. Wild.
J. Phys. G 49, 120502 (2022)
Interpolating between small- and large-g expansions using Bayesian model mixing
A. C. Semposki, R. J. Furnstahl, D. R. Phillips
Phys. Rev. C 106, 044002 (2022)
Uncertainty quantification in breakup reactions
O. Surer, F. M. Nunes, M. Plumlee, S. M. Wild
Phys. Rev. C 106, 024607 (2022)
Model reduction methods for nuclear emulators
J. A. Melendez, C. Drischler, R. J. Furnstahl, A. J. Garcia, Xilin Zhang
J. Phys. G. 49, 102001 (2022)
Analyzing rotational bands in odd-mass nuclei using effective field theory and Bayesian methods
I.K. Alnamlah, E.A. Coello Pérez, D.R. Phillips
Front. in Phys. 10, 901954 (2022)
Performing Bayesian Analyses With AZURE2 Using BRICK: An Application to the 7Be System
D. Odell, C. R. Brune, D. R. Phillips, R. J. deBoer, S. N. Paneru
Front. in Phys. 10, 888746 (2022)
Colloquium: Machine Learning in Nuclear Physics
A. Boehnlein, M. Diefenthaler, C. Fanelli, M. Hjorth-Jensen, T. Horn, M. P. Kuchera, D. Lee, W. Nazarewicz, K. Orginos, P. Ostroumov, L.-G. Pang, A. Poon, N. Sato, M. Schram, A. Scheinker, M. S. Smith,X.-N. Wang, V. Ziegler
Rev. Mod. Phys. 94, 031003 (2022)
Fast emulation of quantum three-body scattering
Xilin Zhang and R. J. Furnstahl
Phys. Rev. C 105, 064004 (2022)
Statistical correlations of nuclear quadrupole deformations and charge radii
Paul-Gerhard Reinhard and Witold Nazarewicz
Phys. Rev. C 106, 014303 (2022)
Prehydrodynamic evolution and its impact on quark-gluon plasma signatures
D. Liyanage, D. Everett, C. Chattopadhyay, U. Heinz
Pnys. Rev. C 105, 064908 (2022)
The Interplay of Femtoscopic and Charge-Balance Correlations
Scott Pratt and Karina Martirosova
Phys. Rev. C 105, 054906 (2022)
Nudged elastic band approach to nuclear fission pathways
Eric Flynn, Daniel Lay, Sylvester Agbemava, Pablo Giuliani, Kyle Godbey, Witold Nazarewicz, Jhilam Sadhukhan
Phys. Rev. C 105, 054302 (2022)
Effective field theory analysis of 3He-alpha scattering data
M. Poudel, D. R. Phillips
J. Phys. G 49, 045102 (2022)
Black Box Variational Bayesian Model Averaging
V. Kejzlar, S. Bhattacharya, M. Son, T. Maiti
The American Statistician (2022)
Efficient emulation of relativistic heavy ion collisions with transfer learning
D. Liyanage, Y. Ji, D. Everett, M. Heffernan, U. Heinz, S. Mak, J-F. Paquet
Physical Review C 105, 034910 (2022)
Statistical tools for a better optical model
M. Catacora-Rios, G. B. King, A. E. Lovell, and F. M. Nunes
Physical Review C 104, 064611 (2021)
Rigorous constraints on three-nucleon forces in chiral effective field theory from fast and accurate calculations of few-body observables
S. Wesolowski, I. Svensson, A. Ekström, C. Forssén, R. J. Furnstahl, J. A. Melendez, and D. R. Phillips
Physical Review C 104, 064001 (2021)
Precision measurement of lightweight self-conjugate nucleus 80Zr
A. Hamaker, E. Leistenschneider, R. Jain, G. Bollen, S. A. Giuliani, K. Lund, W. Nazarewicz, L. Neufcourt, C. R. Nicoloff, D. Puentes, R. Ringle, C. S. Sumithrarachchi, and I. T. Yandow
Nature Physics (2021)
Toward emulating nuclear reactions using eigenvector continuation
C. Drischler, M. Quinonez, P.G. Giuliani, A.E. Lovell, and F.M. Nunes
Physics Letters B 823, 136777 (2021)
Does Bayesian Model Averaging improve polynomial extrapolations? Two toy problems as tests
M. A. Connell, I. Billig, and D. R. Phillips
J. Phys. G 48, 104001 (2021)
Efficient emulators for scattering using eigenvector continuation
R.J. Furnstahl, A.J. Garcia, P.J. Millican, and Xilin Zhang
Physics Letters B 809, 135719 (2020)
Fast & accurate emulation of two-body scattering observables without wave functions
J.A. Melendez, C. Drischler, A.J. Garcia, R.J. Furnstahl, and Xilin Zhang
Physics Letters B 821, 136608 (2021)
Machine-Learning-Based Inversion of Nuclear Responses
K. Raghavan, P. Balaprakash, A. Lovato, N. Rocco, and S.M. Wild
Phys. Rev. C 103, 035502 (2021)