Overview of BAND Framework

The world investment in nuclear physics (NP) has yielded tremendous gains in our understanding of matter as well as many applications that benefit society. Progress in the theory of nuclei and nuclear matter has produced a multitude of models that describe extant data well. But a paradigm shift in the analysis of nuclear-physics data is now necessary: predictions and quantified uncertainties must use the collective wisdom of the best models, constrained by data, and include a unified treatment of all uncertainties. Bayesian Analysis of Nuclei (BAND) will be a set of publicly available software tools—a Cyberinfrastructure Framework—designed to facilitate principled uncertainty quantification (UQ) with multiple nuclear models. It will enable reliable predictions for experimentally inaccessible environments, e.g. the properties and dynamics of matter at the core of neutron stars or in the first microsecond after the Big Bang. And it will make possible quantitative evaluation of the impact of new experiments, so facilitating optimal use of the investment in this science.

The BAND Framework will do this by providing to the community a suite of codes that produce emulators for forefront, computationally-intensive nuclear models, and performs principled uncertainty quantification (UQ) that calibrates those models against data. Codes already exist—some publicly available, some written by members of our team and as yet unpublished—that implement parts of this UQ methodology. But BAND will go further. Because it is built on Bayesian statistical methodology, it will also include a software tool to mix different models, thereby providing a multi-model prediction for key observables. This will permit the use of Bayesian Model Mixing (BMM) as a tool for the quantitative assessment of model-related uncertainties in the multi-model context. A model-mixed prediction that enriches the physics and provides a full assessment of the modeling uncertainty of predictions is a natural outcome within BAND. That prediction includes experimental and modeling errors, thus providing a unified statistical treatment of all uncertainties. That model-mixed prediction can then give insight into what experimental information will best constrain models.

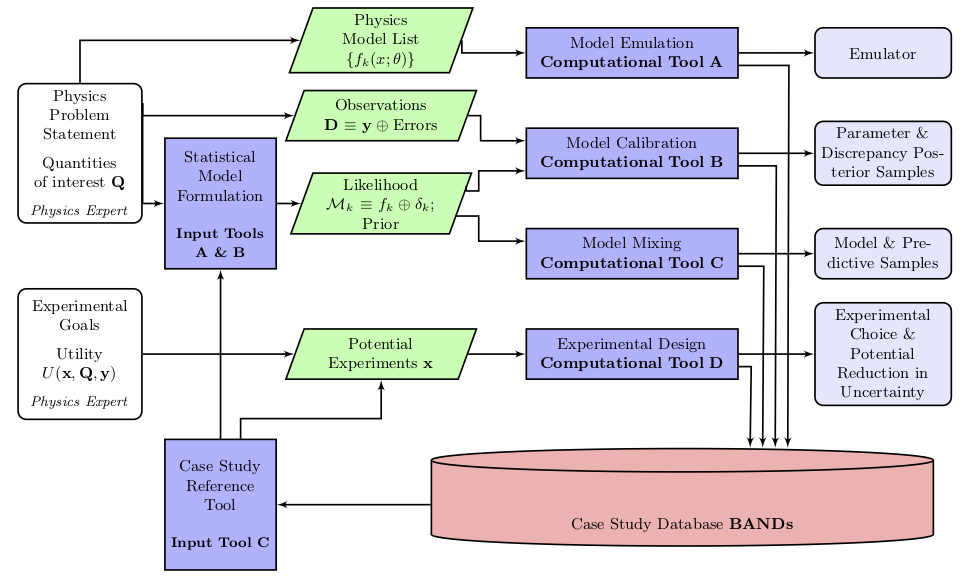
This flowchart illustrates the BAND software framework:

1. The ingredients for Bayesian inference in a nuclear physics—or any—problem include the Bayesian prior, which encodes extrinsic information and expert opinion about the parameters of the model, and the likelihood, which expresses the way in which the data to be considered constrains those parameters. Within BAND, Bayesian statisticians will work with nuclear physicists to develop appropriate formulations of the prior and likelihood. The results will be incorporated into the software framework as Input Tools , and constitute the first step in the flowchart.

2. Nuclear physicists using BAND will also specify the set of models from which they want to obtain a prediction. Very often, these models will be a forefront nuclear-physics calculation that consumes a large amount of supercomputer time to obtain the observables of interest for just one instance of the model parameters. Consequently it is important to build computationally cheap model interpolators for each model. Only then can UQ be accomplished accurately and in a realistic amount of time. This is resolved in the Model Emulation block of the chart (Computational Tool A).

3. Once observed data is also specified by the user, BAND will combine the likelihood and prior and use emulator samples to obtain the posterior probability density function for the parameters of each model in the Model Calibration block (Computational Tool B).

4. Even after calibration and emulation have been achieved, we have still only obtained information on the individual models. Calibrating models to data, while including prior information, is a practice that is gaining increasing currency in nuclear physics. But BAND will push the field further, by taking a set of individual models, each of which have been calibrated to data, and use them to obtain a model-mixed prediction. This will be implemented in Model Mixing block (Computational Tool C).

5. A major challenge in NP, as in many other advanced disciplines, is the optimal design of experiments. Not all measurements are equally useful, and beam time is expensive. The costs of running an experiment include not only the workforce, time and money invested, but also the opportunity cost of alternative measurements that were not carried out. Thus, when planning an experiment, it is important to consider which data are most likely to provide the largest information gain. The process of making the best selection in this regard is known as experimental design. In order to ensure that the substantial resources necessary for modern experiments are focused on acquiring the most valuable data, both the theory uncertainty and the expected pattern of experimental errors must be considered. BAND’s model-mixed prediction is therefore important if nuclear physicists are to have guidance on experimental design that reflects the true extent of model uncertainty. Providing such guidance will be the job of the Experimentation Design block (Computational Tool D).

6. The suite of codes in the BAND Framework will serve a broad community of nuclear physicists, and be coupled with a support database that helps users to apply the framework intelligently and effectively by reliably incorporating their expert prior knowledge. Inferential users usually struggle to borrow information from other similar studies and experimental design users cannot easily get quantitative summaries of what important questions remain in an area. The BAND case study database will give access to both the inputs and the results from previous studies. Case Study Reference will save prior and posterior summaries of parameters of the individual models, hyperparameters in the prior and posterior, model probabilities, and observable posteriors. A new user can use this information to formulate the best priors for her problem, that can then be fed into Statistical Model Formulation. The BAND Framework’s storage of this data also means that likelihoods can be standardized to improve the reproducibility in Statistical Model Formulation.